Understanding Computation (47 page)

This technique can be used to simulate any tag system—including a
tag system that itself simulates a Turing machine—which means that cyclic
tag systems are also
universal.
In 1970,
John Conway invented a
universal system called the
Game of Life
. The “game” is
played on an infinite two-dimensional grid of square cells, each of which can be
alive
or
dead
. A cell is surrounded by its
eight
neighbors
: the three cells above it, the cells to its immediate
left and right, and the three cells below it.
The Game of Life proceeds in a series of
steps like a finite state machine. At every step, each cell
may potentially change from alive to dead, or vice versa, according to
rules that are triggered by the current state of the cell itself and the
states of its neighbors. The rules are simple: a living cell dies if it
has fewer than two living neighbors (underpopulation) or more than three
(overpopulation), and a dead cell comes to life if it has exactly three
living neighbors (reproduction).
Here are six examples
[
63
]
of how the Game of Life rules affect a cell’s state over the
course of a single step, with living cells shown in black and dead ones in
white:
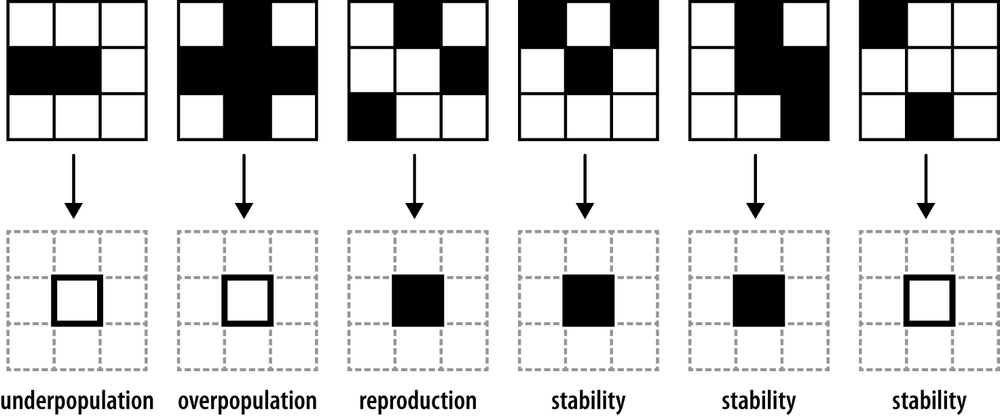
A system like this, consisting of an array of cells and a set of
rules for updating a cell’s state at each step, is called a
cellular automaton
.
Like the other systems we’ve seen in this chapter, the Game of Life
exhibits surprising complexity despite the simplicity of its rules.
Interesting behavior can arise from specific patterns of living cells, the
best-known of which is the
glider
, an arrangement
of five living cells that moves itself one square diagonally across the
grid every four steps:

Many other
significant
patterns
have been discovered, including shapes that move around
the grid in different ways (
spaceships
), generate a
stream of other shapes (
guns
), or even produce
complete copies of themselves (
replicators
).
In 1982, Conway showed how to use a stream of gliders to represent
streams of binary data, as well as how to design logical
And
,
Or
, and
Not
gates to perform digital computation
by colliding gliders in creative ways. These constructions showed that it
was theoretically possible to simulate a digital computer in the Game of
Life, but Conway stopped short of designing a working machine:
For here on it’s just an engineering problem to construct an
arbitrarily large finite (and very slow!) computer. Our engineer has
been given the tools—let him finish the job! […] The kind of computer we
have simulated is technically known as a
universal
machine
because it can be programmed to perform any desired
calculation.—
John Conway,
Winning Ways for Your Mathematical
Plays
In 2002,
Paul Chapman
implemented a
particular kind of universal computer
in Life, and in 2010 Paul
Rendell
constructed a
universal Turing machine
.
Here’s a close-up of one small
part of Rendell’s design:
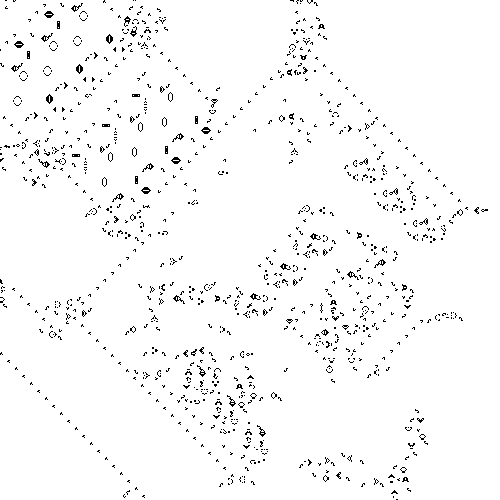
Rule 110
is another
cellular automaton, introduced by
Stephen Wolfram in 1983. Each cell can be either alive or dead, just like the
cells in Conway’s Game of Life, but rule 110 operates on cells arranged in a one-dimensional
row instead of a two-dimensional grid. That means each cell only has two neighbors—the cells
immediately to its left and right in the row—rather than the eight neighbors that surround
each Game of Life cell.
At each step of the rule 110 automaton, the next state of a cell is
determined by its own state and the states of its two neighbors. Unlike
the Game of Life, whose rules are general and apply to many different
arrangements of living and dead cells, the rule 110 automaton has a
separate rule for each possibility:

If we read off the values of the “after” cells from these eight
rules, treating a dead cell as the digit 0 and a living cell as 1, we
get the binary number 01101110. Converting from binary produces the
decimal number 110, which is what gives this cellular automaton its
name.
Rule 110 is much simpler than the Game of Life, but again, it’s capable of complex
behavior. Here are the first few steps of a rule 110 automaton starting from a single live
cell:
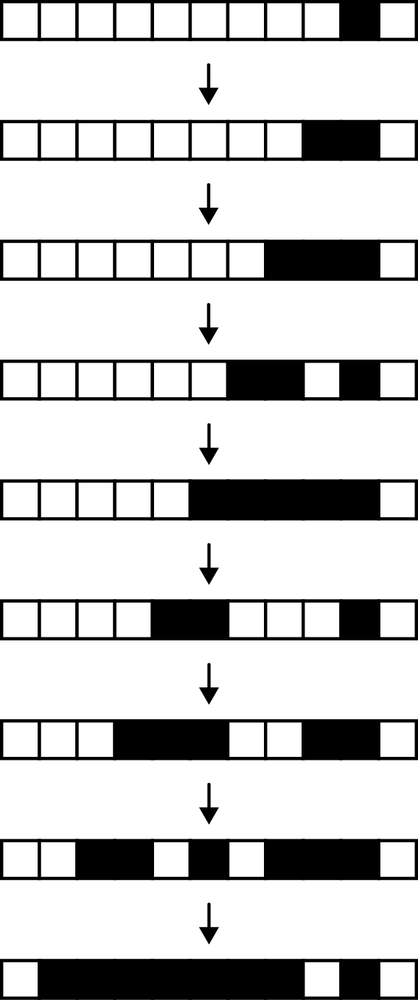
This behavior is already not obviously simple—it’s not just
generating a solid line of living cells, for instance—and if we run the
same automaton for 500 steps we can see interesting patterns begin to
emerge:
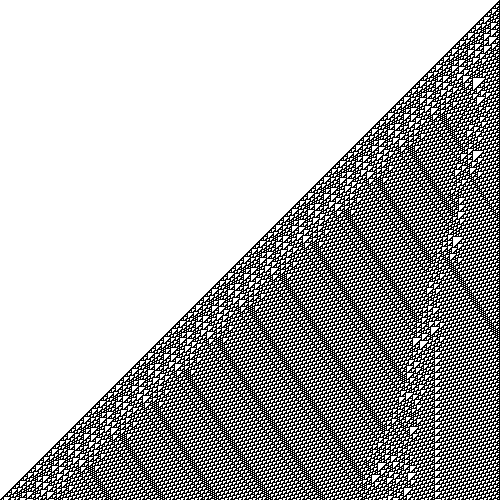
Alternatively, running rule 110 from an initial state consisting of
a random pattern of living and dead cells reveals all kinds of shapes
moving around and interacting with each other:

The complexity that emerges from these eight simple rules turns out
to be remarkably powerful: in 2004, Matthew Cook published a proof that
rule 110 is in fact universal. The proof has a lot of detail (see sections
3 and 4 of
http://www.complex-systems.com/pdf/15-1-1.pdf
) but,
roughly, it introduces several different rule 110 patterns that act as
gliders, then shows how to simulate any cyclic tag system by arranging
those gliders in a particular way.
This means that rule 110 can run a simulation of a cyclic tag system
that is running a simulation of a conventional tag system that is running
a simulation of a universal Turing machine—not an efficient way to achieve
universal computation, but still an impressive technical result for such a
simple cellular automaton.
To complete our whirlwind tour
of simple universal systems, here’s one that’s even simpler
than rule 110:
Wolfram’s 2,3 Turing machine
. It
gets its name from its two states and three characters (a,b, and
blank), which means it has only six rules:
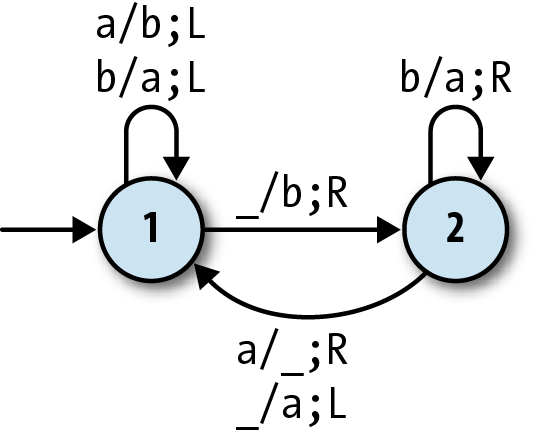
This Turing machine is unusual in that it doesn’t have an accept state, so it never
halts, but this is mostly a technical detail. We can still get results out of nonhalting
machines by watching for certain behavior—for example, the appearance of a particular
pattern of characters on the tape—and treating that as an indication that the current tape
contains useful output.
Wolfram’s 2,3 Turing machine doesn’t seem anywhere near powerful enough to support
universal computation, but in 2007, Wolfram Research announced a $25,000 prize to anyone who
could prove it was universal, and later that year,
Alex Smith
claimed the prize
by
producing a successful proof. As with rule 110, the proof hinges on showing that this machine
can simulate any cyclic tag system; again, the proof is very detailed, but can be seen in
full at
http://www.wolframscience.com/prizes/tm23/
.