Understanding Computation (20 page)

Now the DPDA will gracefully become stuck instead of
blowing up:
>>dpda=DPDA.new(PDAConfiguration.new(1,Stack.new(['$'])),[1],rulebook)=> #>>dpda.read_string('())');dpda.current_configuration=> #, stack=# > >>dpda.accepting?=> false>>dpda.stuck?=> true>>dpda_design.accepts?('())')=> false
While the balanced-brackets
machine does need the stack to do its job, it’s really only using the stack as a
counter, and its rules are only interested in the distinction between “the stack is empty” and
“the stack isn’t empty.” More sophisticated DPDAs will push more than one kind of symbol onto
the stack and make use of that information as they perform a computation. A simple example is
a machine for recognizing strings that contain equal numbers of two characters, sayaandb:
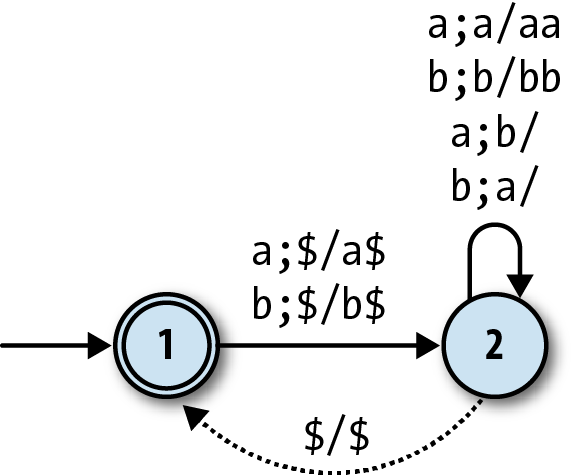
Our simulation shows that it does the job:
>>rulebook=DPDARulebook.new([PDARule.new(1,'a',2,'$',['a','$']),PDARule.new(1,'b',2,'$',['b','$']),PDARule.new(2,'a',2,'a',['a','a']),PDARule.new(2,'b',2,'b',['b','b']),PDARule.new(2,'a',2,'b',[]),PDARule.new(2,'b',2,'a',[]),PDARule.new(2,nil,1,'$',['$'])])=> #>>dpda_design=DPDADesign.new(1,'$',[1],rulebook)=> #>>dpda_design.accepts?('ababab')=> true>>dpda_design.accepts?('bbbaaaab')=> true>>dpda_design.accepts?('baa')=> false
This is similar to the balanced-brackets machine, except its
behavior is controlled by which character is uppermost on the stack. Anaon the top of the stack means that
the machine’s seen a surplus ofas, so
any extraas read from the input will
accumulate on the stack, and eachbread will pop anaoff the stack to
cancel it out; conversely, when there’s abon the stack, it’s thebs that accumulate and theas that cancel them out.
Even this DPDA isn’t taking full advantage of the stack, though. There’s never any
interesting history stored up beneath the top character, just a featureless pile ofas orbs, so we can achieve the
same result by pushing only one kind of character onto the stack (i.e., treating it as a
simple counter again) and using two separate states to distinguish “counting surplusas” from “counting surplusbs”:
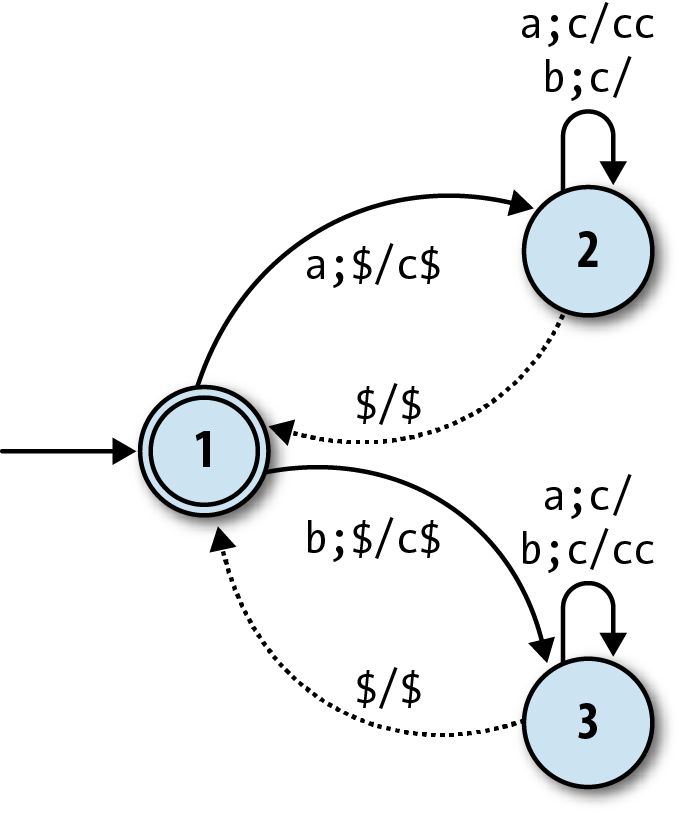
To really exploit the potential of the stack, we need a tougher problem that’ll force us
to store structured information. The classic example is recognizing
palindromes: as we read the input string, character by character, we have to
remember what we see; once we pass the halfway point, we check our memory to decide whether
the characters we saw earlier are now appearing in reverse order. Here’s a DPDA that can
recognize palindromes made up ofaandbcharacters, as long as they have anmcharacter (for “middle”) at the halfway point of the string:
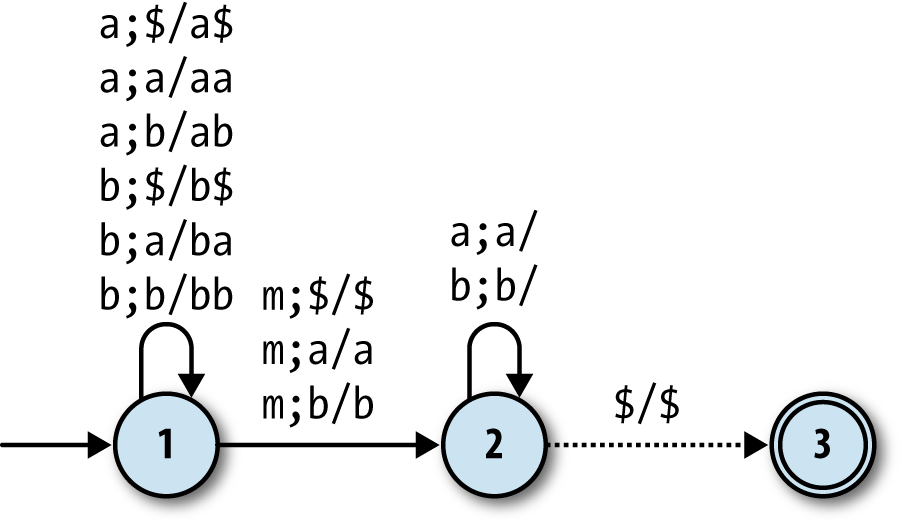
This machine starts in state 1, repeatedly readingas
andbs from the input and pushing them onto the stack. When
it reads anm, it moves into state 2, where it keeps
reading input characters while trying to pop each one
off
the stack. If
every character in the second half of the string matches the stack contents as they’re popped
off, the machine stays in state 2 and eventually hits the$at the bottom of the stack, at which point it moves into state 3 and accepts the input string.
If any of the characters it reads while in state 2 don’t match what’s on the top of the stack,
there’s no rule for it to follow, so it’ll go into a stuck state and reject the string.
We can simulate this DPDA to check that it works:
>>rulebook=DPDARulebook.new([PDARule.new(1,'a',1,'$',['a','$']),PDARule.new(1,'a',1,'a',['a','a']),PDARule.new(1,'a',1,'b',['a','b']),PDARule.new(1,'b',1,'$',['b','$']),PDARule.new(1,'b',1,'a',['b','a']),PDARule.new(1,'b',1,'b',['b','b']),PDARule.new(1,'m',2,'$',['$']),PDARule.new(1,'m',2,'a',['a']),PDARule.new(1,'m',2,'b',['b']),PDARule.new(2,'a',2,'a',[]),PDARule.new(2,'b',2,'b',[]),PDARule.new(2,nil,3,'$',['$'])])=> #>>dpda_design=DPDADesign.new(1,'$',[3],rulebook)=> #>>dpda_design.accepts?('abmba')=> true>>dpda_design.accepts?('babbamabbab')=> true>>dpda_design.accepts?('abmb')=> false>>dpda_design.accepts?('baambaa')=> false