Warped Passages (20 page)

It took time for scientists to sort out the full implications of these experimental observations. The import of quantum mechanics was too radical for most scientists to immediately absorb. Scientists had to suspend their disbelief before they could accept the quantum mechanical premises, which were so different from familiar classical concepts. Even several of the theoretical pioneers, such as Max Planck, Erwin Schrödinger, and Albert Einstein, never really converted to the quantum mechanical way of thinking. Einstein voiced his objection in his famous remark, “God does not play dice with the universe.” Most scientists did eventually accept the truth (as we currently understand it), but not immediately.
The radical nature of the scientific advances in the early twentieth century reverberated in modern culture. The fundamentals of art and literature and our understanding of psychology all changed radically at the time. Although some attribute these developments to the
upheaval and havoc of World War I, artists such as Wassily Kandinsky used the fact that the atom was penetrable to justify the idea that everything can change, and that in art, therefore, everything is allowed. Kandinsky described his reaction to the nuclear atom: “The collapse of the atom model was equivalent, in my soul, to the collapse of the whole world. Suddenly the thickest walls fell. I would not have been amazed if a stone appeared before my eye in the air, melted, and became invisible.”
*
Kandinsky’s reaction was a bit extreme. Radical as the fundamentals of quantum mechanics were, it’s easy to overreach when applying them in nonscientific contexts. I find the most bothersome example to be the frequently abused uncertainty principle, which is often misappropriated to speciously justify inaccuracy. We will see in this chapter that the uncertainty principle is, in fact, a very precise statement about measurable quantities. Nonetheless, it is a statement with surprising implications.
We’ll now introduce quantum mechanics and the underlying principles that make it so different from older,
classical
physics that came before. The strange and new concepts we’ll encounter include quantization, the wavefunction, wave-particle duality, and the uncertainty principle. This chapter outlines these key ideas and gives a flavor of the history of how it was all worked out.
Shock and Awe
The particle physicist Sidney Coleman has said that if thousands of philosophers spent thousands of years searching for the strangest possible thing, they would never find anything as weird as quantum mechanics. Quantum mechanics is difficult to understand because its consequences are so counterintuitive and surprising. Its fundamental principles run counter to the premises underlying all previously known physics—and counter to our own experiences.
One reason that quantum mechanics seems so bizarre is that we are not physiologically equipped to perceive the quantum nature of matter and light. Quantum effects generally become significant at distances of about an angstrom, the size of an atom. Without special instruments, we can see only sizes that are much larger. Even the pixels of a high-resolution television or computer monitor are generally too small for us to see.
Furthermore, we see only huge aggregates of atoms, so many that classical physics overwhelms quantum effects. We generally also perceive only many quanta of light. Although a photoreceptor in an eye is sufficiently sensitive to perceive the smallest possible units of light—individual quanta—an eye typically processes so many quanta that any would-be quantum effects are overwhelmed by more readily apparent classical behavior.
If quantum mechanics is difficult to explain, there is a very good reason. Quantum mechanics is sufficiently far-reaching to incorporate classical predictions, but not the other way round. Under many circumstances—for example, when large objects are involved—quantum mechanical predictions agree with those from classical Newtonian mechanics. But there is no range of size for which classical mechanics will generate quantum predictions. So when we try to understand quantum mechanics using familiar classical terminology and concepts, we are bound to run into trouble. Trying to use classical notions to describe quantum effects is something like trying to translate French into a restricted English vocabulary of only a hundred words. You would frequently encounter concepts or words that could be interpreted only vaguely, or which would be impossible to express at all with such a limited English vocabulary.
The Danish physicist Niels Bohr, one of the pioneers of quantum mechanics, was aware of the inadequacy of human language for describing the inner workings of the atom. Reflecting on the subject, he related how his models “had come to him intuitively…as pictures.”
*
As the physicist Werner Heisenberg explained, “We simply have to remember that our usual language does not work any more,
that we are in the realm of physics where our words don’t mean much.”
*
I will therefore not attempt to describe quantum phenomena with classical models. Instead, I will describe the key fundamental assumptions and phenomena that made quantum mechanics so different from the classical theories that came before. We’ll reflect individually on several of the key observations and insights that contributed to quantum mechanics and its development. Although this discussion follows a roughly historical outline, my real purpose is to introduce the many new ideas and concepts intrinsic to quantum mechanics one at a time.
The Beginning of Quantum Mechanics
Quantum physics developed in stages. It began as a series of random assumptions that matched observations, although no one understood why they matched. These inspired guesses, which had no underlying physical justification but did have the virtue of giving the right answers, were embodied in what is now known as the
old quantum theory
. This theory was defined by the assumption that quantities such as energy and momentum couldn’t have just any arbitrary values. Instead, the possibilities were confined to a discrete,
quantized
set of numbers.
Quantum mechanics, which developed from the humble antecedent of the old quantum theory, justifies the mysterious quantization assumptions that we’ll shortly encounter. Furthermore, quantum mechanics provides a definite procedure for predicting how quantum mechanical systems evolve with time, greatly increasing the theory’s power. But at the outset quantum mechanics developed only in fits and starts, since no one at the time really understood what was going on. At first, the quantization assumptions were all there were.
The old quantum theory began in 1900, when the German physicist
Max Planck suggested that light could be delivered only in quantized units, just as bricks can only be sold in discrete chunks. According to Planck’s hypothesis, the amount of energy contained in light of any specific frequency could only be a multiple of the fundamental energy unit for that particular frequency. That fundamental unit is equal to a quantity, now known as Planck’s constant,
h
, multiplied by the frequency,
f
. The energy of light with a definite frequency
f
could be
hf
, 2
hf
, 3
hf
, and so on, but according to Planck’s assumption you could never find anything in between. Unlike bricks, whose quantization is arbitrary and nonfundamental—bricks can be split apart—there is a minimum energy unit of light of a given frequency which is indivisible. Intermediate values of energy could never occur.
This remarkably prescient suggestion was made to address a theoretical puzzle known as the blackbody
ultraviolet
*
catastrophe
. A blackbody is an object, such as a piece of coal, that absorbs all incoming radiation and then radiates it back.
†
The amount of light and other energy it emits depends on its temperature; temperature completely characterizes a blackbody’s physical properties.
However, the classical predictions for the light radiated from a blackbody were problematic: classical calculations predicted that far greater energy would be emitted in high-frequency radiation than physicists had seen and recorded. Measurements showed that different frequencies do not contribute democratically to blackbody radiation; the very high frequencies contribute less than the lower ones. Only the lower frequencies emit significant energy. This is why radiating objects are “red-hot” and not “blue-hot.” But classical physics predicted a large amount of high-frequency radiation. In fact, the total emitted energy predicted by classical reasoning was infinite. Classical physics faced an ultraviolet catastrophe.
An ad hoc way out of this dilemma would have been to assume that only frequencies below some specific upper limit could contribute to radiation from a blackbody. Planck disregarded this possibility in
favor of another, apparently equally arbitrary, assumption: that light is quantized.
Planck reasoned that if radiation at each frequency consisted of whole-unit multiples of a fundamental quantum of radiation, then no high-frequency radiation could be emitted because the fundamental unit of energy would be too large. Because the energy contained in a quantum unit of light was proportional to frequency, even a single unit of high-frequency radiation would contain a large amount of energy. When the frequency was high enough, the minimum energy a quantum would contain would be too large for it to be radiated. The blackbody could radiate only the lower-frequency quanta. Planck’s hypothesis thereby forbade excessive high-frequency radiation.
An analogy might help elucidate Planck’s logic. You’ve probably eaten dinner with people who protest when it is time to order dessert. They’re afraid of eating too much fattening food, so they rarely order their own tasty treats. If the waiter promises that the desserts are small, they might order one. But they quail at the usual large, quantized portions of cake or ice cream or pudding.
There are two types of such people. Ike belongs to the first category. He has true discipline, and really doesn’t eat dessert. When a dessert is too big, Ike simply refrains from eating it. I’m more like the second type of person—Athena is also one—who thinks that the desserts are too big, and therefore doesn’t order any for herself, but, unlike Ike, has no compunction about taking bites from the desserts on everyone else’s plate. So even when Athena refuses to order her own portion, she still ends up eating quite a lot. If Athena were eating dinner with a large number of people, and hence could pick off a large number of plates, she would suffer from an unfortunate “calorie catastrophe.”
According to the classical theory, a blackbody is more like Athena. It would emit small amounts of light at any frequency, and theorists using classical reasoning would therefore predict an “ultraviolet catastrophe.” To avoid this predicament, Planck suggested that a blackbody was analogous to the truly abstemious type. Like Ike, who never eats a fraction of a dessert, a blackbody behaves according to Planck’s quantization rule and emits light of a given frequency only in quantized energy units, equal to the constant
h
times the frequency
f
. If the frequency were high, the quantum of energy would be simply too big for light to be emitted at that frequency. A blackbody would therefore emit most of its radiation at low frequencies, and high frequencies would be automatically cut out. In quantum theory, a blackbody doesn’t emit a substantial amount of high-frequency radiation and therefore emits far less radiation than is predicted by the classical theory.
When an object emits radiation, we call the radiation pattern—that is, how much energy the object emits at each frequency at a given temperature—its
spectrum
10
(see Figure 40). The spectra of certain objects such as stars can approximate that of a blackbody. Such blackbody spectra have been measured at many different temperatures, and they all agree with Planck’s assumption. Figure 40 shows that the emission is all at lower frequency; at high frequency, emission shuts off.
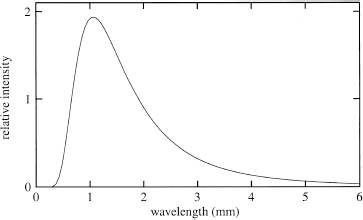
Figure 40.
The blackbody spectrum of the cosmic microwave background of the universe. A blackbody spectrum gives the amount of light that is emitted at all frequencies when the temperature of the radiating object is fixed. Notice that the spectrum cuts off at high frequency.
One of the great achievements of experimental cosmology since the 1980s has been the increasingly accurate measurement of the blackbody spectrum that the radiation in our universe produces. Originally, the universe was a hot, dense fireball containing high-temperature radiation, but since then the universe has expanded and the radiation has cooled tremendously. That is because as the universe
expanded, the wavelengths of the radiation did too. And longer wavelength corresponds to lower frequency, which corresponds to lower energy, which also corresponds to lower temperature. The universe now contains radiation that looks as if it has been produced by a blackbody with a temperature of only 2.7 degrees above absolute zero—considerably cooler than when it started.