Warped Passages (23 page)

Figure 45.
The interference pattern that is recorded in the double slit experiment. The four panels on the left show, clockwise from the top left, the pattern seen after 50, 500, 5, 000, and 50, 000 electrons have been shot through. The curves on the right compare the distribution of the number of electrons (upper curve) to the pattern you would get for a wave that passes through the two slits. They are nearly identical, which shows that the electron wavefunction does in fact act like a wave.

But how can the double-slit experiment indicate that an individual electron acts like a wave, when we already know that electrons are particles? After all, there is no such thing as half an electron. Any individual electron gets recorded in a definite location. What’s really going on?

The answer is the one I gave earlier. You can see the wave pattern only when you record many electrons. Each individual electron is a particle. It hits the screen in a single location. However, the cumulative effect of many electrons being shot at the screen is a classical wave pattern, reflecting the fact that the two electron paths interfere. You can see this in Figure 45.

The wavefunction gives the probability that an electron will hit the screen in any particular location. The electron might go anywhere, but you would expect to find it only at some particular place with a definite probability given by the value of the wavefunction at that point. Many electrons together produce the wave that you could derive from the assumption that the electron passes through both slits.

In the 1970s, Akira Tonamura in Japan and Piergiorgio Merli,
Giulio Pozzi, and Gianfranco Missiroli in Italy actually saw this explicitly in real experiments. They shot electrons through one at a time and saw the wave pattern develop as more and more electrons hit the screen.

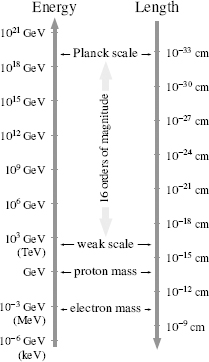
Figure 46.
Some important length scales and energy scales in particle physics. Larger energies correspond (via special relativity and the uncertainty principle) to smaller distances—a more energetic wave is sensitive to interactions that occur over shorter distance scales. The gravitational interaction is inversely proportional to the Planck scale energy. The large Planck scale energy means that gravitational interactions are weak. The weak scale energy is the energy which sets the scale (via
E = mc
²
) for the weak gauge boson masses. The weak scale length is the distance over which the weak gauge bosons communicate the weak force.

You might wonder why it took until the twentieth century for anyone to notice something as dramatic as wave-particle duality. For example, why didn’t people realize any earlier that light looks like a wave but is actually composed of discrete nuggets—namely, photons?

The answer is that none of us (with the possible exception of
superheroes) sees individual photons,
^*
so quantum mechanical effects cannot be easily detected. Ordinary light doesn’t look as if it’s made up of quanta. We see bunches of photons that constitute visible light. The large number of photons together act as a classical wave.

You need a very weak source of photons, or a very carefully prepared system, to observe the quantized nature of light. When there are too many photons, you can’t distinguish the effect of any single one. Adding one more photon to classical light, which contains many photons, just doesn’t make a big enough difference. If your lightbulb, which behaves classically, emitted one additional photon, you would never notice. You can observe detailed quantum phenomena only in carefully prepared systems.

If you don’t believe that this one last photon is usually insignificant, think about how you feel when you go to the voting booth. Is it really worth the time and trouble to vote when you know that your vote can’t possibly make a difference in the outcome, since millions of other people are voting? With the notable exception of Florida, the state of uncertainty, one vote generally gets lost in the crowd. Even though an election gets decided by the cumulative effect of individual votes, a single vote rarely, if ever, changes the result. (And, to take the comparison a step further, you might also observe that only in quantum systems—and in Florida, which acts like a quantum state—do repeated measurements produce different results.)

Heisenberg’s Uncertainty

The wave nature of matter has many counterintuitive implications. We’ll now turn from electoral uncertainty to Heisenberg’s uncertainty principle, a favorite of physicists and after-dinner speakers.

The German physicist Werner Heisenberg was one of the major pioneers of quantum mechanics. In his autobiography, he told how
his revolutionary ideas about atoms and quantum mechanics began to germinate when he was headquartered in the Theological Training College in Munich, where he was stationed in 1919 to fight off Bavarian communists. After the shooting had subsided, he sat on the college roof and read Plato’s dialogues, the
Timaeus
in particular. Plato’s text convinced Heisenberg that “in order to interpret the material world, we need to know something about its smallest parts.”
^*

Heisenberg hated the external upheaval that surrounded him in his youth; he would have preferred a return to “the principles of Prussian life, the subordination of individual ambition to the common cause, modesty in private life, honesty and incorruptibility, gallantry and punctuality.”
^†
Nonetheless, with the uncertainty principle Heisenberg irrevocably changed people’s worldview. Perhaps the tumultuous era in which Heisenberg lived gave him a revolutionary approach to science, if not to politics.
^‡
In any case, I find it a little ironic that the author of the uncertainty principle was a man of such conflicting dispositions.

The uncertainty principle says that certain pairs of quantities can never be measured accurately at the same time. This was a major departure from classical physics, which assumes that, at least in principle, you can measure all the characteristics of a physical system—position and momentum, for example—as accurately as you’d like.

The particular pairs are those for which it matters which one you measure first. For example, if you were to measure position and then momentum (the quantity which gives both speed and direction), you wouldn’t get the same result as if you first measured momentum and then position. This would not be the case in classical physics, and is certainly not what we are used to. The order of measurements matters only in quantum mechanics. And the uncertainty principle says that for two quantities where the order of measurement matters, the product of the uncertainties of the two will always be greater than a
fundamental constant, namely Planck’s constant,
h
, which is 6.582 × 10
^-25
GeV second for those who want to know.
^*
12
If you insist on knowing position very accurately, you cannot know momentum with a similar accuracy, and vice versa. No matter how precise your measuring instruments and no matter how many times you try, you can never simultaneously measure both quantities to very high accuracy.

The appearance of Planck’s constant in the uncertainty principle makes a good deal of sense. Planck’s constant is a quantity that arises only with quantum mechanics. Recall that, according to quantum mechanics, the quanta of energy of a particle with a particular frequency is Planck’s constant times that frequency. If classical physics ruled the world, Planck’s constant would be zero and there would be no fundamental quantum.

But in the true quantum mechanical description of the world, Planck’s constant is a fixed, nonzero quantity. And that number tells us about uncertainty. In principle, any individual quantity can be accurately known. Sometimes physicists refer to the
collapse of the wavefunction
to specify that something has been accurately measured and therefore takes a precise value. The word “collapse” refers to the shape of the wavefunction, which is no longer spread out but takes a nonzero value at one particular place, since the probability of measuring any other value afterwards is zero. In this case—when one quantity is measured precisely—the uncertainty principle would tell you that after the measurement, you can know nothing at all about the other quantity that is paired with the measured quantity in the uncertainty principle. You would have infinite uncertainty in the value of that other quantity. Of course, had you first measured the second quantity, the first quantity would be the one you didn’t know. Either way, the more accurately you know one of the quantities, the less precise the measurement of the other has to be.

I won’t go into the detailed derivation of the uncertainty principle in this book, but I’ll nonetheless try to give a flavor of its origin. Because this is not essential to what follows, feel free to skip ahead to the next section. But you might want to learn a little more about the reasoning that underlies uncertainty.

In this derivation, we’ll focus on time-energy uncertainty, which is a little easier to explain and understand. The time-energy uncertainty principle relates the uncertainty in energy (and hence, according to Planck’s assumption, frequency) to the time interval that is characteristic of the rate of change of the system. That is, the product of the energy uncertainty and the characteristic time for the system to change will always be greater than Planck’s constant,
h
.

A physical realization of the time-energy uncertainty principle happens, for example, when you turn on a light switch and hear static from a nearby radio. Turning on the light switch generates a large range of radio frequencies. That’s because the amount of electricity going through the wire changed very rapidly, so the range of energy (and hence frequency) must be large. Your radio picks it up as static.

To understand the uncertainty principle’s origin, let’s now consider a very different example—a leaky faucet.
^*
We will show that you need a long-lasting measurement to accurately determine the rate at which the faucet drips, which we will see is closely analogous to the uncertainty principle’s claim. A faucet and the water passing through it, which involve many atoms, is too complex a system to exhibit observable quantum mechanical effects—they are overwhelmed by classical processes. It is nonetheless true that you need longer measurements to make more accurate frequency determinations—and that is the core of the uncertainty principle. A quantum mechanical system would take this interdependence a step further because for a carefully prepared quantum mechanical system, energy and frequency are related. So for a quantum mechanical system, a relation between frequency uncertainty and the length of time of a measurement (like the one we are about to see) therefore translates into the true uncertainty relation between energy and time.

Suppose that water is dripping at a rate of about once per second. How well could you measure the rate if your stopwatch had one-second accuracy—that is, it could be off by at most one second? If you were to wait one second, and saw a single drip, you might think that you could conclude that the faucet drips once per second.

However, because your stopwatch could be off by as much as one second, your observation wouldn’t tell you precisely how long it took for the faucet to drip. If your watch ticked once, the time might have been a little more than one second, or it might have been nearly two. At what time, between one and two seconds, should you say the faucet dripped? Without a better stopwatch or a longer measurement, there would be no preferred answer. With the watch you have, you can conclude only that the drops fall somewhere in the range between one per second and one per two seconds. If you said that the faucet drips once per second, you could have essentially 100% error in your measurement. That is, you could be off by as much as a factor of two.

But suppose that instead you waited 10 seconds while performing your measurement. Then, 10 drops of water would have fallen during the time it took your watch to click 10 times. With your crude stopwatch with only 1-second accuracy, all you could really infer is that the time it took for 10 drips was somewhere between 10 and 11 seconds. Your measurement, which would again say that the drips fall approximately once per second, would now have an error of only 10%. That’s because by waiting 10 seconds, you could measure frequency to within 1/10 of a second. Notice that the product of the time for your measurement (10 seconds) and the uncertainty in frequency (10 %, or 0. 1) is was roughly 1. Notice also that the product of uncertainty in frequency and time for the measurement in the first example, which had more error in the frequency measurement (100 %) but took place over a shorter time (1 second), is also about 1.

You could continue along these lines. If you were to perform a measurement for 100 seconds, you could measure frequency to an accuracy of water dripping once per 100 seconds. If you were to measure water dripping for 1,000 seconds, you could measure frequency with an accuracy of once per 1,000 seconds. In all these cases the product of the time interval over which you performed your measurement and the accuracy with which you measure frequency is about 1.
^*
The longer time required for a more accurate measurement of frequency is at the heart of the time-energy uncertainty principle.
You can measure frequency more accurately, but to do so you would have to measure for longer. The product of time and the uncertainty in frequency is always about 1.
^*