Warped Passages (4 page)

Figure 3.
The one-dimensional Sam plot.
Let’s explore this notion a little further. Icarus Rushmore III (Ike in the above story), a Boston resident, is a more complex character. In fact, he is three dimensional. Ike is twenty-one, drives fast cars, and loses money at Wonderland, a town near Boston with a dog-racing track. In Figure 4 I’ve plotted Ike. Although I’ve drawn it on the two-dimensional surface of a piece of paper, the three axes tell us that Ike is definitely three-dimensional.
*
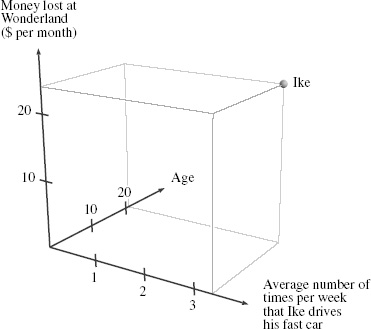
Figure 4.
The three-dimensional Ike plot. The solid notched lines are the coordinate axes of the three-dimensional plot. The point that is labeled Ike corresponds to a 21-year-old boy who loses 24 dollars at Wonderland every month and drives his fast car (on average) 3.3 times a week.
When we describe most people, however, we usually assign them more than one, or even three, characteristics. Athena, Ike’s sister, is
an eleven-year-old who reads avidly, excels at math, keeps abreast of current events, and raises pet owls. You might want to plot this too (though why, exactly, I’m not really sure). In that case, Athena would have to be plotted as a point in a five-dimensional space with axes corresponding to age, number of books read per week, average math test score, number of minutes spent reading the newspaper per day, and number of owls she owns. However, I’m having trouble drawing such a graph. It would require a five-dimensional space, which is very hard to draw. Even computer programs only have 3D graphics.
Nonetheless, in an abstract sense, there exists a five-dimensional space with a collection of five numbers, such as (11, 3, 100, 45, 4), which tells us that Athena is eleven, that she reads three books on the average each week, that she never gets a math question wrong, that she reads the newspaper for forty-five minutes each day, and that she has four owls at the moment. With these five numbers, I’ve described Athena. If you knew her, you could recognize her from this point in five dimensions.
The number of dimensions for each of the three people above was the number of attributes I used to identify them: one for Sam, three for Ike, and five for Athena. Real people, of course, are generally more difficult to capture with so few items of information.
In the following chapters, we’ll use dimensionality to explore not people, but space itself. By “space” I mean the region in which matter exists and physical processes take place. A
space of a particular dimension
is a space requiring a particular number of quantities to specify a point. In one dimension, that would be a point on a plot with a single
x
axis; in two dimensions, a point on a plot with an
x
and a
y
axis; in three dimensions, it would be a point on a plot with an
x
, a
y
, and a
z
axis.
1,
*
Those axes are shown in Figure 5.
In three-dimensional space, three numbers are all you ever need to know your precise location. The numbers you specify might be latitude, longitude, and altitude; or length, width, and height; or you might have a different way to choose your three numbers. The critical thing is that three dimensions means you need precisely three numbers.
In two-dimensional space you need two numbers, and in higher-dimensional space you need more.
Figure 5.
The three coordinate axes that we use for three-dimensional space.
More dimensions means freedom to move in a greater number of completely different directions. A point in a four-dimensional space simply requires one additional axis—again, difficult to draw. But it should not be hard to imagine its existence. We’ll think about it using words and mathematical terms.
String theory suggests even more dimensions: it postulates six or seven extra spatial dimensions, meaning that six or seven additional coordinates are needed to plot a point. And very recent work in string theory has shown that there could be even more dimensions than that. In this book, I’ll keep an open mind and entertain the possibility of any number of extra dimensions. It is too soon to say how many dimensions the universe actually contains. Many of the concepts about extra dimensions that I will describe apply to any number of extra dimensions. In the rare cases when that isn’t true, I will make sure that it is clear.
Describing a physical space involves more than just identifying points, however. You need also to specify a
metric
, which establishes the measurement scale, or the physical distance between two points. These are the markings along the axis of a graph. It’s not enough to know that the distance between a pair of points is 17 unless you know whether 17 means 17 centimeters, 17 miles, or 17 light-years. A metric is required to tell us how to measure distance: what the distance
between two points on a graph corresponds to in the world that the graph represents. A metric gives a measuring rod that reveals your choice of units in order to set the scale, just like on a map, where a half-inch might represent one mile, or as in the metric system, which gives us a meter stick we all agree on.
But that is not all a metric specifies. It also tells us whether space bends or curls around, like the surface of a balloon when it is blown up into a sphere. The metric contains all the information about the shape of space. A metric for curved space tells us about both distances and angles. Just as an inch can represent different distances, an angle can correspond to different shapes. I’ll go into this later on when we explore the connection between curved space and gravity. For now, let’s just say that the surface of a sphere is not the same as the surface of a flat piece of paper. Triangles on one don’t look like triangles on the other, and the difference between these two-dimensional spaces can be seen in their metrics.
2
As physics has evolved, so has the amount of information stored in the metric. When Einstein developed relativity, he recognized that a fourth dimension—time—is inseparable from the three dimensions of space. Time, too, needs a scale, so Einstein formulated gravity by using a metric for four-dimensional
spacetime
, adding the dimension of time to the three dimensions of space.
And more recent developments have shown that additional spatial dimensions might also exist. In that case, the true spacetime metric will involve more than three dimensions of space. The number of dimensions and the metric for those dimensions is how one describes such a multidimensional space. But before we explore metrics and metrics for multidimensional spaces any further, let’s think more about the meaning of the term “multidimensional space.”
Playful Passages Through Extra Dimensions
In Roald Dahl’s
Charlie and the Chocolate Factory
, Willy Wonka introduced visitors to his “Wonkavator.” In his words, “An elevator can only go up and down, but a Wonkavator goes sideways and slantways and longways and backways and frontways and squareways
and any other ways that you can think of…”
*
Really, what he had was a device that moved in any direction, so long as it was a direction in the three dimensions we know. It was a nice, imaginative idea.
However, the Wonkavator didn’t really go any way “you can think of.” Willy Wonka was remiss in that he neglected extra-dimensional passages. Extra dimensions are other directions entirely. They are hard to describe, but they may be easier to understand by analogy.
In 1884, to explain the notion of extra dimensions, the English mathematician Edwin A. Abbott wrote a novel called
Flatland
.
†
It takes place in a fictitious two-dimensional universe—the Flatland of the title—where two-dimensional beings (of various geometric shapes) reside. Abbott shows us why Flatlanders, who live their whole lives in two dimensions—on a table top, for example—are as mystified by three dimensions as people in our world are by the idea of four.
For us, more than three dimensions requires a stretch of the imagination, but in Flatland three dimensions are beyond its inhabitants’ comprehension. Everyone thinks it is obvious that the universe holds no more than their two perceived dimensions. Flatlanders are as insistent about this as most people here are about three.
The book’s narrator, A. Square (the namesake of the author, Edwin A
2
), is introduced to the reality of a third dimension. In the first stage of his education, while he is still confined to Flatland, he watches a three-dimensional sphere travel vertically through his two-dimensional world. Because A. Square is confined to Flatland, he sees a series of disks that increase and then decrease in size, which are slices of the sphere as it passes through A. Square’s plane (see Figure 6).
This is initially perplexing to the two-dimensional narrator, who has never imagined more than two dimensions and has never contemplated a three-dimensional object like a sphere. It is not until A. Square has been lifted out of Flatland into the surrounding three-dimensional world that he can truly imagine a sphere. From his new perspective, he recognizes the sphere as the shape made by gluing together the two-dimensional slices he witnessed. Even in his two-dimensional
world, A. Square could have plotted the disks he sees as a function of time (as in Figure 6) to construct the sphere. But it wasn’t until his trip through a third dimension opened his eyes that he fully comprehended the sphere and its third spatial dimension.
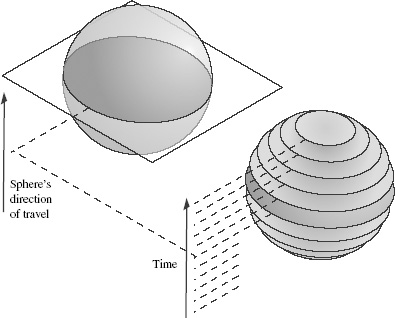
Figure 6.
If a sphere passes through a plane, a two-dimensional observer would see a disk. The sequence of disks that the observer sees over time comprises the sphere.
By analogy, we know that if a
hypersphere
(a sphere with four spatial dimensions) were to pass through our universe, it would appear to us as a time sequence of three-dimensional spheres that increase, then decrease, in size.
3
Unfortunately, we don’t have the opportunity to journey through an extra dimension. We will never see a static hypersphere in its entirety. Nonetheless, we can make deductions about how objects look in spaces of different dimensions—even dimensions that we don’t see. We can confidently deduce that our perception of a hypersphere passing through three dimensions would look like a series of three-dimensional spheres.
As another example, let’s imagine the construction of a
hypercube
—a generalization of a cube to more than three dimensions. A line segment of one dimension consists of two points connected
by a straight, one-dimensional line. We can generalize this in two dimensions to a square by putting one of these one-dimensional line segments above another and connecting them with two additional segments. We can generalize further in three dimensions to a cube, which we can construct by placing one two-dimensional square above the other and connecting them with four additional squares, one on each edge of the original squares (see Figure 7).