Warped Passages (6 page)

Figure 12. Portrait of Dora Maar,
a cubist painting by Picasso.

Figure 13.
Dali’s
Crucifixion (Corpus Hypercubus)
.
Most Western painters since the Renaissance, however, have used perspective and shading to create the illusion of a third dimension. One of the essential skills in painting is the ability to reduce a three-dimensional world to a two-dimensional representation that allows the observer to reverse the process and reconstitute the initial three-dimensional scene or object. We are acculturated to know how to decode the images, even though not all of the three-dimensional information is there.
Artists have even tried representing higher-dimensional objects on two-dimensional surfaces. For example, Salvador Dali’s
Crucifixion (Corpus Hypercubus)
(see Figure 13) shows the cross as an opened-up hypercube. A hypercube consists of eight cubes attached in four-dimensional space. These are the cubes he has drawn. I’ve shown a few projections of a hypercube in Figure 14.
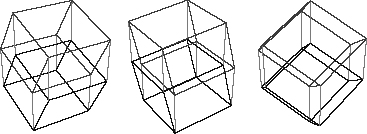
Figure 14.
Projections of a hypercube.
I have already mentioned a physics example: quasicrystals, which look like the projection of a higher-dimensional crystal into our three-dimensional world. Projections can also be used for practical, not just artistic purposes. Medicine contains many examples where three-dimensional objects are projected onto two dimensions. An X-ray always records a two-dimensional projection. CAT (computer-assisted tomography) scans combine multiple X-ray images to reconstruct a more informative three-dimensional representation. With X-rays taken from sufficiently many angles, one can use interpolation to piece together full three-dimensional images. An MRI (magnetic
resonance imaging) scan, on the other hand, reconstructs a three-dimensional object from slices.
A holographic image is another way to record three dimensions on a two-dimensional surface. Although a holographic image is recorded on a lower-dimensional surface, it actually carries all the information of the original higher-dimensional space. You probably have an example of this technique in your wallet: the three-dimensional-looking image on your credit card is a hologram.
A holographic image records relationships between light in different places, so that the full higher-dimensional image can be recovered. This principle is much the same as that used in a good stereo, which lets you hear where instruments were being played in relation to each other when they were recorded. With the information stored in a hologram, the eye can truly reconstruct the three-dimensional object it represents.
These methods tell us how we might get more information from a lower-dimensional image. But maybe all you really need is less information. Sometimes you just don’t care about all three dimensions. For example, something might be so thin in the third dimension that nothing interesting happens in this direction: even though the ink on this paper is really three-dimensional, we lose nothing by thinking of it as two-dimensional. Unless we look at the page under a microscope, we simply don’t have the necessary resolution to see the ink’s thickness. A wire looks one-dimensional even though, on closer inspection, you can see it has a two-dimensional cross-section and therefore three dimensions in all.
Effective Theories
There is nothing wrong with ignoring an extra dimension that’s too small to be seen. Not only the visual effects, but also the physical effects of tiny, undetectable processes can usually be ignored. Scientists often average over or ignore (often unwittingly) physical processes that occur on immeasurably small scales when formulating their theories or setting up their calculations. Newton’s laws of motion work at the distances and speeds he could observe. He didn’t need the
details of general relativity to make successful predictions. When biologists study a cell, they don’t need to know about quarks inside the proton.
Selecting relevant information and suppressing details is the sort of pragmatic fudging everyone does every day. It’s a way of coping with too much information. For almost anything you see, hear, taste, smell, or touch, you have the choice between examining details by scrutinizing very closely, and looking at the “big picture” with its other priorities. Whether you are staring at a painting, tasting wine, reading philosophy, or planning your next trip, you automatically parcel your thoughts into the categories of interest—be they sizes or flavors or ideas—and the categories that you don’t find relevant at the time. When appropriate, you ignore some details so that you can focus on the issue of interest, and not obscure it with inessential details.
This procedure of disregarding small-scale information should be familiar because it’s actually a conceptual leap people make all the time. Take New Yorkers, for example. New Yorkers living in the thick of the city see the details and variation within Manhattan. To them, downtown is funkier, older, with narrower, more crooked streets. Uptown has more real estate that was designed for human beings to actually live in, as well as Central Park and most of the museums. Although such distinctions are blurred from far away, within the city they are very real.
But now think about how people far away see New York. To them, it’s a dot on a map. An important dot, perhaps, a dot with a distinctive character; but from outside New York, a dot nonetheless. Even with all their variety, New Yorkers are in a single category when viewed from the Midwest or Kazakhstan, for example. When I mentioned this analogy to my cousin who lives downtown (in the West Village, to be precise), he confirmed my point by balking at the suggestion of grouping together New Yorkers living uptown and downtown. Nonetheless, as any non-New Yorker could tell him, the distinctions are too small to matter to people not living in their midst.
It is common practice in physics to formalize this intuition, and organize categories in terms of the distance or energy that is relevant. Physicists accept this practice and have given it a name—
effective theory
. The effective theory concentrates on the particles and forces
that have “effects” at the distance in question. Rather than describing particles and interactions in terms of unmeasurable parameters that describe ultra-high-energy behavior, we formulate observations in terms of the things that are actually relevant to the scales we might detect. The effective theory at any single distance scale doesn’t go into the details of an underlying short-distance physical theory; it only asks about things you could hope to measure or see. If something is beyond the resolution of the scales at which you are working, you don’t need its detailed structure. This practice is not scientific fraud, but a way of disregarding the clutter of superfluous information. It is an “effective” way to obtain accurate answers efficiently.
Everyone, including physicists, is happy to return to a three-dimensional universe when higher-dimensional details are beyond our resolution. Just as physicists will often treat a wire as if it is one-dimensional, we will also describe a higher-dimensional universe in lower-dimensional terms when the extra dimensions are minuscule and higher-dimensional details are too tiny to matter. Such a lower-dimensional description would summarize the observable effects of all possible higher-dimensional theories in which the extra dimensions are too tiny to see. For many purposes, such a lower-dimensional description is adequate, independent of the number, size, and shape of the additional dimensions.
The lower-dimensional quantities are not providing the fundamental description, but they are a convenient way of organizing observations and predictions. If you do know the short-distance details, or the microstructure, of a theory, you can use them to derive the quantities that appear in the low-energy description. Otherwise, those quantities are just unknowns to be experimentally determined.
The following chapter elaborates these ideas and considers the consequences of tiny rolled-up extra dimensions. The dimensions we’ll consider first are minuscule, too tiny to make any difference at all. Later on, when we return to extra dimensions, we’ll explore both the large and the infinite dimensions that recently radically revised this picture.
Restricted Passages: Rolled-up Extra Dimensions
No way out
None whatsoever.
Jefferson Starship
Athena awoke with a start. The previous day she had read
Alice in Wonderland
and
Flatland
in order to seek some inspiration about dimensions. But that night she had the strangest dream, which, when fully conscious, she recognized as the result of having read the two books on the same day.
*
Athena dreamed she had turned into Alice, slipped into a rabbit hole, and met the resident Rabbit, who had pushed her out into an unfamiliar world. Athena had thought it a rather rude way to convey a guest. Even so, she had eagerly looked forward to her upcoming adventure in Wonderland.
Athena was in for a disappointment, however. The resident Rabbit, who was fond of puns, had sent her instead to OneDLand, a strange, not so wonderful, one-dimensional world. Athena looked around—or, I should say, to her left and right—and discovered that all she could see were two points—one to her left and another to her right (but in a prettier color, she thought).
In OneDLand, all the one-dimensional people with their one-dimensional possessions were lined up along this single dimension like long, thin beads strung out along a thread. But even with her limited purview, Athena knew there must be more to OneDLand than met her eyes because of the outrageous din that met her ears. A Red Queen was well hidden behind a dot, but Athena couldn’t miss her strident yells: “This is the most ridiculous chess game I have ever seen! I can’t move any pieces, not even to castle!” Athena was relieved when she realized her one-dimensional existence shielded her from the wrath of the Red Queen.
But Athena’s cozy universe did not last long. Slipping through a gap in OneDLand, she returned to the dreamworld’s rabbit hole, which had an elevator that could take her to hypothetical, other-dimensional universes. Almost immediately, the Rabbit announced, “Next stop: TwoDLand—a two-dimensional world.” Athena didn’t think “TwoDLand” a very nice name, but she cautiously entered all the same.
Athena needn’t have been so hesitant. Almost everything in TwoDLand looked the same as in OneDLand. She did notice one difference—a vial labeled “Drink me.” Bored with one dimension, Athena promptly obeyed. She quickly shrank to a tiny size, and as she became smaller, a second dimension came into view. This second dimension was not very big—it was wrapped around in a fairly small circle. Her surroundings now resembled the surface of an extremely long tube. A Dodo was racing around this circular dimension, but he wanted to stop. So he kindly offered Athena, who looked rather hungry, some cake.
When Athena ate a morsel of the Dodo’s dreamcake, she started to grow. After only a few bites (she was quite sure of this, as she was still rather hungry), the cake very nearly disappeared; all that remained was a very tiny crumb. At least Athena thought there was a crumb, but she could see it only when she squinted very hard. And the cake wasn’t the only thing that had vanished from view: when Athena returned to her usual size, the entire second dimension had disappeared.
She thought to herself, “TwoDLand is very odd indeed. I’d best be getting home.” Her return journey was not without further adventures, but those will be kept for another time.
Even if we don’t know
why
three spatial dimensions are special, we can ask
how
. How is it possible that the universe could appear to have only three dimensions of space if the fundamental underlying spacetime contains more? If Athena is in a two-dimensional world, why does she sometimes see only one? If string theory is the correct description of nature, and there are nine dimensions of space (plus one of time), what has become of the missing six spatial dimensions? Why aren’t they visible? Do they have any discernible impact on the world we see?