Warped Passages (7 page)

The last three questions are central to this book. However, the first order of business is to determine whether there is any way in which the evidence of extra dimensions can be hidden so that Athena’s two-dimensional world would appear as one-dimensional, or a universe with extra dimensions would appear to have the three-spatial-dimensional structure we observe around us. If we’re to accept the idea of a world with extra dimensions, whatever theory they come from, there must be a good explanation for why we have not yet detected even the slightest trace of their existence.

This chapter is about extremely small
compactified
, or rolled-up, dimensions. They don’t extend for ever, like the three familiar dimensions; instead, they quickly loop back on themselves, like a tightly wound spool of thread. No two objects could be separated very far along a compactified dimension; any attempt at a long-distance excursion would instead turn into a journey that went round and round, like the Dodo’s laps. Such compactified dimensions could be so small that we wouldn’t ever notice their existence. Indeed, we’ll see that if tiny rolled-up dimensions exist, they will be quite a challenge to detect.

Rolled-up Dimensions in Physics

String theory, the most promising candidate for a theory combining quantum mechanics and gravity, gives a concrete reason to think about extra dimensions: the only coherent versions of string theory that we know of are laden with these surprising appendages. However, although the arrival of string theory in the physics world improved
the respectability of extra dimensions, the idea of extra dimensions originated much earlier.

Back in the early twentieth century, Einstein’s theory of relativity opened the door to the possibility of extra dimensions of space. His theory of relativity describes gravity, but it doesn’t tell us why we experience the particular gravity we do. Einstein’s theory does not favor any particular number of spatial dimensions. It works equally well for three or four or ten. Why, then, do there seem to be only three?

In 1919, close on the heels of Einstein’s theory of general relativity (completed in 1915), the Polish mathematician Theodor Kaluza recognized this possibility in Einstein’s theory and boldly proposed a fourth spatial dimension, a new unseen dimension of space.
^*
He suggested that the extra dimension somehow might be distinguished from the three familiar infinite ones, though he didn’t specify how. Kaluza’s goal with this extra dimension was to unify the forces of gravity and electromagnetism. Although the details of that failed unification attempt are irrelevant here, the extra dimension that he had so brazenly introduced is very relevant indeed.

Kaluza wrote his paper in 1919. Einstein, who was the referee evaluating it for publication in a scientific journal, wavered about the merits of the idea. Einstein delayed the publication of Kaluza’s paper for two years, but eventually acknowledged its originality. Yet Einstein still wanted to know what this dimension was. Where was it and why was it different? How far did it extend?

These are the obvious questions to ask. They might be some of the very same questions that are bothering you. No one responded to Einstein until 1926, when the Swedish mathematician Oskar Klein addressed his questions. Klein proposed that the extra dimension would be curled up in the form of a circle, and that it would be extremely small, just 10
^-33
cm,
^†
one tenth of a millionth of a trillionth
of a trillionth of a centimeter. This tiny rolled-up dimension would be everywhere: each point in space would have its own minuscule circle, 10
^-33
cm in size.

This small quantity represents the Planck length, a quantity that will be relevant later when we discuss gravity in more detail. Klein picked the Planck length because it is the only length that could naturally appear in a quantum theory of gravity, and gravity is connected to the shape of space. For now, all you need to know about the Planck length is that it is extraordinarily, unfathomably small—far smaller than anything we would ever have a chance of detecting. It is about twenty-four orders of magnitude
^†
smaller than an atom and nineteen orders of magnitude smaller than a proton. It’s easy to overlook anything as tiny as that.

There are many examples in daily life of objects whose extent in one of the three familiar dimensions is too small to be noticed. The paint on a wall, or a clothesline viewed from far away, are examples of things that seem to extend in fewer than three dimensions. We overlook the paint’s depth and the clothesline’s thickness. To a casual observer, the paint looks as if it has only two dimensions, and the clothesline appears to have only one, even though we know that actually both have three. The only way to see the three-dimensional structure of such things is to look up close, or with sufficiently fine resolution. If we stretched a hose across a football field and viewed it from a helicopter above, as is illustrated in Figure 15, the hose would look one-dimensional. But up close, you can resolve the two dimensions of the hose’s surface and the three-dimensional volume it encloses.

For Klein, though, the thing that was undiscernibly small was not the thickness of an object, but a dimension itself. So what does it mean for a dimension to be small? What would a universe with a
curled-up dimension look like to someone living inside it? Once again, the answer to these questions depends entirely on the size of the curled-up dimension. Let’s consider an example to see what the world would look like to conscious beings that are small or big compared with the size of a rolled-up extra dimension. Because drawing four or more spatial dimensions is impossible, the first picture I’ll present of a universe with a small, compactified dimension will have only two dimensions, with one of them rolled up tightly to a very small size (see Figure 16).

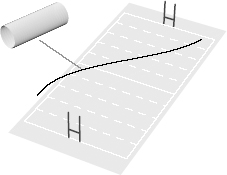
Figure 15.
When you view a hose spread over a football field from above, it looks like it has one dimension. But when you view it up close, you see that the surface has two dimensions and the volume it encloses has three.

Figure 16.
When one dimension is curled up, a two-dimensional universe looks one-dimensional.

Imagine again a garden hose, which can be thought of as a long sheet of rubber rolled up into a tube with a small circular cross-section. This time, we’ll think of the hose as the entire universe (not an object
inside the universe).
^*
If the universe were shaped like this garden hose, we would have one very long dimension and one very small, rolled-up dimension—exactly what we want.

For a little creature—a flat bug, say—that lived in the garden-hose universe, the universe would look two-dimensional. (In this scenario, our bug has to stick to the surface of the hose—the two-dimensional universe doesn’t include the interior, which is three-dimensional.) The bug could crawl in two directions: along the length of the hose or around it. Like the Dodo, who could run laps in its two-dimensional universe, a bug that started somewhere along the hose could crawl around and eventually return to where it started. Because the second dimension is small, the bug wouldn’t travel very far before it returned.

If a population of bugs living on the hose experienced forces, such as the electric force or gravity, those forces would be able to attract or repel bugs in any direction on the surface of the hose. Bugs could be separated from one another either along the length of the hose or around the hose’s circumference, and would experience any force that was present on the hose. Once there is sufficient resolution to distinguish distances as small as the diameter of the hose, forces and objects exhibit both of the dimensions they actually have.

However, if our bug could observe its surroundings, it would notice that the two dimensions were very different. The one along the length of the hose would be very big. It could even be infinitely long. The other dimension, on the other hand, would be very small. Two bugs could never get very far from each other in the direction around the hose. And a bug that tried to take a long trip in that direction would quickly end up back where it started. A thoughtful bug that liked to stretch its legs would know that its universe was two-dimensional, and that one dimension extended a long way while the other was very small and rolled up into a circle.

But the bug’s perspective is nothing like the one that creatures like
us would have in Klein’s universe, in which the extra dimension is rolled up to an extremely small size, 10
^-33
cm. Unlike the bug, we are not small enough to detect—never mind travel in—a dimension of such a tiny size.

So to complete our analogy, suppose that something much bigger than a bug, capable only of much coarser resolution and therefore unable to detect small objects or structure, lived in the garden-hose universe. Since the lens through which this bigger being views the world blurs any details that are as small as the hose’s diameter, from the vantage point of this bigger being the extra dimensions would be invisible. It would see only a single dimension. Someone would see that the garden-hose universe had more than a single dimension only if he had sufficiently sharp vision to register something as small as the width of the hose. If his vision is too fuzzy to register that width, all he’ll ever notice is a line.

Moreover, physical effects wouldn’t betray the extra dimension’s existence. Big beings in the garden-hose universe would fill out the entire second, small dimension and would never know that this dimension was there. Without the ability to detect structure or variations along the extra dimension, such as wiggles or undulations of matter or energy, they could never register its existence. Any variations along the second dimension would be completely washed out, much as any variation in the thickness of a piece of paper on the scale of its atomic structure is something you don’t ever notice.

The two-dimensional world in which the dreaming Athena found herself was very much like the garden-hose universe. Because Athena had the opportunities to be both big and small relative to TwoDLand’s width, she could observe this universe from both the perspective of someone bigger and that of someone smaller than its second dimension. To the big Athena, TwoDLand and OneDLand appeared the same in every respect. Only the small Athena could tell the difference. Similarly, in the garden-hose universe a being would be ignorant of an additional spatial dimension if it were too tiny for it to see.

Let’s now return to the Kaluza-Klein universe, which has the three spatial dimensions we know about, supplemented by an extra one that’s unseen. We can again use Figure 16 to think about this situation. Ideally, I would draw four spatial dimensions, but unfortunately that’s
not possible (even a pop-up book wouldn’t suffice). However, since the three infinite dimensions that constitute our space are all qualitatively the same, I really need only draw just one representative dimension. That leaves me free to use the other dimension to represent the unseen extra dimension. The other dimension shown here is the one that’s curled up—the one that’s fundamentally different from the other three.

Just as with our two-dimensional garden-hose universe, a four-dimensional Kaluza-Klein universe with a single tiny, rolled-up dimension would appear to us to have one dimension fewer than the four it actually has. Because we wouldn’t know about the additional spatial dimension unless we could detect evidence of structure on its minute scale, the Kaluza-Klein universe would look three-dimensional. Rolled-up, or compactified, extra dimensions will never be detected if they are sufficiently tiny. Later on, we’ll investigate just
how
tiny, but for now, rest assured that the Planck length is well below the threshold of detectability.

In life, and in physics, we only register those details that actually matter to us. If you cannot observe detailed structure, you might as well pretend it isn’t there. In physics, this disregard of local detail is embodied in the effective theory idea of the previous chapter. In an effective theory, all that matters are the things that you can actually perceive. In the example above, we would use a three-dimensional effective theory where the information about extra dimensions is suppressed.