Warped Passages (61 page)

Figure 79.
A filled-in funnel consists of flat slices glued together.

A simpler way of illustrating the curvature of warped spacetime is through the shape of the graviton’s probability function. The graviton is the particle that communicates the gravitational force, and its probability function tells us the likelihood of finding the graviton at any fixed position in space. The strength of gravity is reflected in this function: the larger its value, the stronger the graviton’s interactions at that particular point, and the stronger the force of gravity.

For flat spacetime, the graviton would be equally likely to be found anywhere. The probability function for a graviton in flat spacetime would therefore be constant. But for curved spacetime, as in the
warped geometry we are considering, this would no longer be the case. Curvature tells us about the shape of gravity. When spacetime is curved, the value of the graviton’s probability function is different at different locations in spacetime.

Because each slice of spacetime is completely flat in our warped geometry, the graviton’s probability function doesn’t vary along the three standard spatial dimensions—it changes only along the fifth dimension.
^*
In other words, even though the graviton’s probability function has different values at different places along the fifth dimension, so long as two points are equally far along the fifth dimension, the value will be the same. This tells us that the graviton’s probability function depends only on position in the fifth dimension. Nonetheless, it completely characterizes the warped spacetime’s curvature. And because that function varies only with a single coordinate, that of the fifth dimension, it is simple to plot.

This graviton’s probability function along the fifth dimension is shown in Figure 80. It decreases exponentially quickly, which is to say extraordinarily rapidly, as one leaves the first brane, which we
will call the Gravitybrane, and heads towards the second brane, which we’ll call the Weakbrane. The Gravitybrane and the Weakbrane are different because the first carries positive energy, while the second carries negative energy. And this energy assignment makes the graviton’s probability function much bigger in the vicinity of the Gravitybrane.

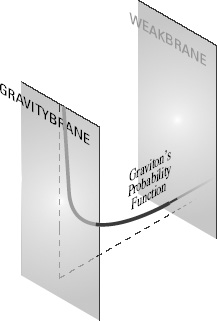
Figure 80.
The graviton’s probability function falls off exponentially as it moves away from the Gravitybrane and towards the Weakbrane.

The effect of the plummeting probability function is that the graviton, the physical particle whose exchange generates gravitational attraction, has very little chance to be found near the Weakbrane. The graviton’s interactions on the Weakbrane are therefore highly suppressed.

The strength of gravity depends so strongly on position along the fifth dimension that the strengths of gravity experienced on the two branes, which border the opposite ends of this warped five-dimensional world, are extraordinarily different. Gravity is strong on the first brane, where gravity is localized, but feeble on the second, where the Standard Model resides. Because the graviton’s probability function is negligibly small on the second brane, the graviton’s interactions with Standard Model particles, which are confined there, are extremely weak.

This tells us that in this warped spacetime we would actually expect to find a hierarchy between observed masses and the Planck scale mass. Although the graviton is everywhere, it interacts with far greater strength with particles on the Gravitybrane than with particles on the Weakbrane. The graviton just isn’t hanging around there all that much. The graviton’s probability function on the Weakbrane is extremely tiny, and if this scenario is the correct description of the world, this tinyness is responsible for the feebleness of gravity in our world.

In this model, feeble gravity on the Weakbrane doesn’t require a large separation between the two branes. Once you leave the Gravitybrane, where the graviton’s probability function is highly concentrated, gravity becomes exponentially weaker, which makes gravity on the Weakbrane extremely feeble. Because the graviton’s probability function is falling precipitously, gravity is highly suppressed on the Weakbrane (where we live). It can be ten million billion times weaker than you would expect without the warping, even if the
two branes are fairly close together. This aspect of the theory, the fact that the branes don’t need to be separated by very much, makes this model a far more realistic possibility than large extra dimensions. Although large extra dimensions were a tantalizing rephrasing of the hierarchy problem, at the end of the day they still leave an unexplained large number—the extra dimensions’ size. In the theory we are now considering, the gravitational force on the Weakbrane is many orders of magnitude weaker than other forces, even when the Weakbrane is only a modest distance away from the first brane (the Gravitybrane).

The distance between branes in this warped geometry need only be a little larger than the Planck scale length. Whereas the large dimensions scenario required the introduction of an extremely large number—namely the size of the dimensions—in the warped geometry, no contrived large number is required to explain the hierarchy. That is because an exponential automatically turns a modest number into an extremely huge number (the exponential) or an extremely tiny one (the inverse of the large exponential). The strength of gravity is smaller on the Weakbrane; it is reduced by a factor of the exponential of the distance between the two branes.
^*
The enormous ratio between the Planck scale mass—the large mass that tells us that gravity is weak—and the mass of the Higgs particle, and therefore the masses of the weak gauge bosons, is expected if the Weakbrane is located at distance of 16 units away,
^†
since the ratio of the different masses is about 10
¹⁶
(ten million billion). That means that a distance between the branes that is only about a factor of sixteen bigger than your most naive guess would suffice to explain the hierarchy. A factor of sixteen might sound big, but it is a lot smaller than ten million billion, the number we are trying to explain.

For years, particle physicists had hoped to find an exponential explanation of the hierarchy. That is, we had hoped to interpret the previously unexplained large number as the consequence of a
naturally occurring exponential function. Now, with extra dimensions, Raman and I had found a way for particle physics to automatically incorporate an exponential hierarchy of masses. The interaction of gravity could be much smaller at the location of our brane, the Weakbrane, than it would be where the graviton’s probability function peaks. Because gravity on our brane would be weakened by the warped geometry, if the Standard Model is housed on the Weakbrane, the hierarchy problem would be solved. This was a solution to the hierarchy problem, and it had fallen right into our laps.

Another way to understand this remarkable new feature of the warped geometry is to consider how gravity gets diluted. In Chapter 19, we explained the weakness of gravity in the ADD scenario in terms of the gravitational force lines emitted from a massive object, which were diluted because they were spread throughout large dimensions. If we so chose, we could have described this dilution as a consequence of the graviton’s probability function. Remember that the graviton’s probability function tells us how gravity is spread out over space. Because gravity in the large extra-dimensions scenario is equally strong everywhere in the extra dimensions, the graviton’s probability function in this case is flat. Such a flat graviton probability function would tell us that the graviton, the particle communicating gravity, is spread out over the large region enclosed by the extra dimensions. This flat probability function, that is equally distributed over all of extra-dimensional space, tells us that gravity’s influence in four dimensions is vastly diluted.

In the warped five-dimensional spacetime we are now considering, there is an interesting twist. The graviton no longer has equal probability of being in all places in five-dimensional space that lie between its two boundaries, the Gravitybrane and the Weakbrane. The distribution of the graviton is in fact far from democratic as an automatic consequence of the energy carried by the branes and in the bulk. The graviton’s probability function varies: it is big in one region and small in all others, and it is this variation that provides the dilution factor responsible for making gravity so weak in our world. Gravity is feeble on the Weakbrane because the graviton’s probability function there is so minuscule.

Let us momentarily return to the sprinkler analogy that we used earlier to explain how the strength of gravity decreases with distance. The larger the region over which the sprinkler distributes water (as illustrated in the upper part of Figure 81), the more the water gets diluted. When there are large extra dimensions, gravity is spread over a very big region, and it too gets diluted. Gravity therefore appears to be feeble in the low-energy, effective four-dimensional theory.

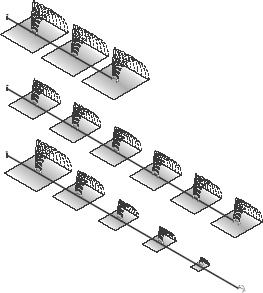
Figure 81.
Three different sprinklers. By comparing the first and second sprinklers, we see that a longer sprinkler delivers less water over any particular region than a shorter one does. The third sprinkler demonstrates that water can be inequitably distributed so that the first garden always gets half the water, the second garden one-quarter, and so on. In that case, the amount of water delivered to the first garden is independent of the sprinkler’s length; it always gets half the water.

The warped geometry, on the other hand, resembles a sprinkler that does not distribute water equally in all directions, but instead delivers it preferentially to one particular region, the region around the
Gravitybrane (see the lower part of Figure 81). With an undemocratic sprinkler, it is obvious that less water will be delivered everywhere aside from the favored region. And, if the amount of water delivered to other regions falls off exponentially from the highly favored location, the water fraction delivered to those other areas will be very tiny indeed, even if they are only a modest distance away. Clearly, the water delivered by the “warped” sprinkler is “diluted” far more than water that is equally distributed to all regions.

The upshot is that if all the Standard Model particles are housed on the Weakbrane, then gravity is so weak compared with the other three forces that the hierarchy problem of particle physics, the question of why gravity is so weak relative to the other forces, is solved. Feeble gravity is a natural consequence of the small amplitude of the graviton’s probability function on the Weakbrane, even when it is only a relatively modest distance (about ten times larger than the string-theory-favored Planck scale length) away from the Gravitybrane.

Growing and Shrinking in a Warped Dimension

The previous explanation of the hierarchy in terms of the exponentially falling probability function is entirely adequate for understanding warped spacetime. The intuitive explanation for the weakness of gravity is that the graviton is less likely to be found on the Weakbrane. You are free to accept this explanation and skip to the next section, but you might want to read the following, slightly more rigorous explanation, which delves further into the fascinating properties of warped spacetime.

In this section, we’ll see that gravity’s weakness on the Weakbrane can also be explained as a consequence of objects getting bigger and lighter as you move away from the Gravitybrane and approach the Weakbrane. Were Athena to move from the Gravitybrane to the Weakbrane (as she will in the story in the next chapter), she would see her shadow on the Gravitybrane increase in size as she moved away. And the amount her shadow would increase is enormous—it would grow by sixteen orders of magnitude!

We will also see that in this geometry, heavy and light particles can peacefully coexist. Even when there are Planck-scale-mass particles on one of the two branes, there are only weak-scale-mass particles on the other. Therefore, there is no longer a hierarchy problem.