Warped Passages (66 page)

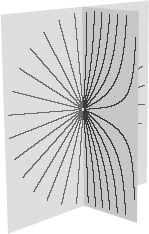
Figure 89.
In the warped scenario, the field lines are equally distributed in all the directions on the brane. However, off the brane the field lines bend back around so that they become essentially parallel to the brane, almost as if the fifth dimension were finite. Even with an infinite dimension, the gravitational field is localized near the brane, and field lines spread essentially as if there were only four (spacetime) dimensions.
To show that the size of the fifth dimension is irrelevant to the strength of gravity near the brane, we would want to show that the first few gardens get very nearly the same amount of water, regardless of whether we stop delivering water when we get to the fifth garden or the tenth garden or we don’t stop delivering water at all. So let’s consider what happens if the sprinkler ended after the first five gardens. Because the sixth garden and beyond would have received so little water, the total amount of water that the sprinkler would send to the first several gardens would differ from that of an infinite sprinkler by only a few percent. And if you stopped the sprinkler after the seventh garden, it would differ by even less. With our distribution
of water where nearly all the water is used on the first several gardens, the faraway gardens, which receive only a very tiny fraction of the water, are irrelevant to the amounts of water the first few gardens receive.
*
Because I will use the duck analogy again in the next chapter, I’ll explain the same thing in terms of counting ducks attracted to the shore where someone has sprinkled crumbs. If you were to first count nearby ducks, and then count ones a little further out, your duck counting would quickly become almost futile. By the time you get a little way away from shore, there would be very few ducks left to count. You don’t need to keep counting ducks far from the shore because you’ve already counted essentially all of them by focusing on the region near the shore (see Figure 88).
The graviton’s probability function is simply so small beyond the second brane that a second brane’s location would make only a negligible difference to the interaction strength of the four-dimensional graviton. In other words, the extent of the fifth dimension is immaterial to the apparent strength of four-dimensional gravity in this theory, in which the gravitational field is localized near the Gravitybrane.
37
Even if there’s no second brane and the fifth dimension is infinite, gravity still looks four-dimensional.
Raman and I called our scenario
localized gravity
. That is because the graviton’s probability function is localized near a brane. Although, strictly speaking, gravity can leak out into the fifth dimension because the fifth dimension is indeed infinite, in reality it does not because of the low probability of the graviton being found far away. Space is not truncated, yet everything remains in a concentrated region in the vicinity of the brane. A faraway brane makes no difference to physical processes on the Gravitybrane since very little from the Gravitybrane ventures far away. Anything produced on or near the Gravitybrane remains nearby, in a localized region.
Sometimes physicists refer to this model of localized gravity as RS2. The RS stands for Randall and Sundrum, but the 2 is misleading—it refers to the fact that this was the second paper we wrote on warped geometry, not the fact that there are two branes. The scenario with two branes, which addresses the hierarchy problem, is known as RS1. (The names would be less confusing if we had written the papers in the opposite order.) Unlike RS1, the scenario in this chapter is not necessarily relevant to the hierarchy problem, though you can introduce a second brane and solve the hierarchy as well, as we briefly considered towards the end of Chapter 20. But whether or not there is a second brane inside the space to address the hierarchy problem, localized gravity is a radical possibility with important theoretical implications that contradicts the long-held assumption that extra dimensions must be compact.
Kaluza-Klein Partners of the Graviton
The previous section discussed the graviton’s probability function, which is heavily concentrated on the Gravitybrane. The particle I was talking about plays the role of the four-dimensional graviton because it travels almost exclusively along the brane and has only a tiny probability of leaking out into the fifth dimension. From the graviton’s perspective, space looks as if the fifth dimension is only 10
-33
cm in size (a size set by the curvature, which is in turn set by the energy in the bulk and on the brane) rather than of infinite extent.
But although Raman and I were rather excited by our discovery, we weren’t sure that we had completely solved the problem. Was the localized graviton by itself sufficient to generate a four-dimensional effective theory in which gravity behaved as it would in four dimensions? The potential problem was that Kaluza-Klein partners of the graviton could also contribute to the gravitational force, and could thereby significantly modify gravity.
The reason this seemed so dangerous was that, generally, the larger the size of the extra dimension, the smaller the mass of the lightest KK particle. For our theory with an infinite dimension, this would
mean that the lightest KK particle could be arbitrarily light. And because the difference in masses of the KK particles also decreases with the size of the extra dimension, infinitely many types of very light graviton KK partners could be produced at any finite energy. All these KK particles could potentially contribute to the gravitational force law and change it. The problem looked especially bad because even if each KK particle interacted very weakly, if there were too many of them then the gravitational force would nonetheless look quite different from that in four dimensions.
On top of that, since the KK particles are extremely light, they might be easy to produce. Colliders already operate at sufficiently high energy to make them. Even ordinary physical processes, such as chemical reactions, would generate enough energy to create graviton KK partners. If the KK particles carried too much energy to the five-dimensional bulk, the theory would be ruled out.
Fortunately, neither of these concerns turns out to be a problem. When we calculated the probability functions for the KK particles, we found that the graviton KK partners interact extremely weakly on or near the Gravitybrane. Despite the large number of graviton KK partners, they all interact so feebly that there is no danger of producing too many of them or of changing the form of the gravitational force law anywhere. If there is any problem at all, it is that this theory so closely mimics four-dimensional gravity that we don’t yet know any way to distinguish it experimentally from a truly four-dimensional world! The graviton KK partners would have such a negligible impact on anything observable that we do not yet know how to tell the difference between four flat dimensions and four flat dimensions supplemented by a fifth, warped one.
You can understand the weakness of the graviton KK partners’ interactions from the shape of their probability functions. As with the graviton, these tell us the likelihood of any particle being found at any position along the fifth dimension. Raman and I followed the more or less standard procedure for finding the masses and probability functions of each graviton KK partner in our warped geometry. This involved solving a quantum mechanics problem.
For a flat fifth dimension, the quantum mechanics problem,
described in Chapter 6, was to find the waves that fit around the rolled-up dimension and thereby quantize the allowed energies.
*
For our warped, infinite fifth-dimensional geometry, the quantum mechanics problem looked rather different, since we needed to take into account the energy on the brane and in the bulk that warped spacetime. But we were able to modify the standard procedure to suit our setup. The results were fascinating.
The first KK particle we found was the one with no momentum in the fifth dimension. The probability function of this particle is heavily concentrated on the Gravitybrane and decreases exponentially away from it. This shape should sound familiar: it is the probability function for the same four-dimensional graviton we have already discussed. This massless KK mode is the four-dimensional graviton that communicates Newton’s four-dimensional force law.
The remaining KK particles are very different, however. None of these other KK particles are likely to be found near the Gravitybrane. Instead, what you find is that for any value of mass between zero and the Planck scale mass, there exists a KK particle with that particular mass, and the probability function for each of those particles peaks at a different place along the fifth dimension.
In fact, there is an interesting interpretation for the locations of the different peaks. We saw in Chapter 20 that in warped spacetime, in order to put all particles on the same footing in the four-dimensional effective theory so that they all interact with gravity in the same way, we rescaled all distances, times, energies, and momenta differently along the fifth dimension. As one travels out away from the brane, each point gets associated with an exponentially smaller energy. That was why particles on the Weakbrane were expected to have a mass of about a TeV. The shadow of Athena traveling out into the fifth dimension became bigger, and Athena became lighter, as she moved from the Gravitybrane toward the Weakbrane.
Each point along the fifth dimension can be associated with a particular mass in the same way; the mass is related to the Planck
scale mass by the rescaling at that point. And the KK particle whose gravity function peaks at a particular point has approximately that rescaled Planck scale mass. As you travel out into the fifth dimension, you encounter successively lighter KK particles whose probability functions peak there.
In fact, you might say that the Kaluza-Klein spectrum exhibits a highly segregated society. Heavy KK particles are banished from the regions of space where the rescaled energy is too small to produce them. And light KK particles are rarely found in those regions that contain very energetic particles. KK particles concentrate as far from the Weakbrane as they can, given their mass. Their locations are like the size of teenage boys’ pants, which are as baggy as they can be without falling down. Fortunately, the physical laws that determine the KK particles’ locations are easier to understand than the far more perplexing rules of teenage fashion.
For us, the most important feature of the probability functions for the light KK particles is that they are extremely small on the Gravitybrane. That means there is only a small probability of finding light KK particles on or near there. Because light KK particles shy away as much as possible from the Gravitybrane, light particles (aside from the exceptional graviton whose probability function peaks on the Gravitybrane) would only rarely be produced there. Furthermore, light KK particles don’t significantly modify the gravitational force law because they tend to stay away from the Gravitybrane and therefore don’t interact much with brane-bound particles.
Putting everything together, Raman and I decided that we had found a theory that worked. The Gravitybrane-localized graviton is responsible for the appearance of four-dimensional gravity. Despite the abundance of KK graviton partners, they interact so weakly on the Gravitybrane that their effect is not at all noticeable. And despite the existence of an infinite fifth dimension, all physical laws and processes, including that of gravity, appear to agree with what is expected of a four-dimensional world. In this highly warped space, an infinite extra dimension is permissible.
As mentioned earlier, if anything, this model is frustrating from an observational vantage point. Amazing as it may seem, this five-dimensional model mimics four dimensions so extraordinarily well
that it will be extremely difficult to tell them apart. Particle physics experimenters will certainly have a hard time.
Physicists have, however, begun to explore astrophysical and cosmological features that might distinguish the two worlds. Many physicists
*
have considered black holes in the warped spacetime and they continue to investigate whether there exist distinguishing features that we can use to determine which type of universe we actually live in.
As of now, we know that localization is a new and fascinating theoretical possibility for extra dimensions in our universe. I eagerly look forward to further developments that could ultimately determine whether it’s a true feature of our world.
What’s New
- A dimension can be infinitely long, yet be invisible, if spacetime is suitably warped.
- Gravity can be localized, even if it is not strictly confined to a finite region.
- In localized gravity, the massless KK particle is the localized graviton. It is concentrated close to the Gravitybrane.
- All other KK particles are concentrated far from the Gravitybrane; the shape of their probability function and the locations where they peak depend on their mass.