Zero (6 page)
Authors: Charles Seife

Pythagoras's doctrine became the centerpiece of Western philosophy: all the universe was governed by ratios and shapes; the planets moved in heavenly spheres that made music as they turned. But what lay beyond these spheres? Were there more and more spheres, each larger than its neighbor? Or was the outermost sphere the end of the universe? Aristotle and later philosophers would insist that there could not be an infinite number of nested spheres. With the adoption of this philosophy, the West had no room for infinity or the infinite. They rejected it outright. For the infinite had already begun to gnaw at the roots of Western thought, thanks to Zeno of Elea, a philosopher reckoned by his contemporaries to be the most annoying man in the West.
Zeno was born around 490
BC
, at the beginning of the Persian warsâa great conflict between East and West. Greece would defeat the Persians; Greek philosophy would never quite defeat Zenoâfor Zeno had a paradox, a logical puzzle that seemed intractable to the reasoning of Greek philosophers. It was the most troubling argument in Greece: Zeno had proved the impossible.
According to Zeno, nothing in the universe could move. Of course, this is a silly statement; anyone can refute it by walking across the room. Though everybody knew that Zeno's statement was false, nobody could find a flaw in Zeno's argument. He had come up with a paradox. Zeno's logical puzzle baffled Greek philosophersâas well as the philosophers who came after them. Zeno's riddles plagued mathematicians for nearly two thousand years.
In his most famous puzzle, “The Achilles,” Zeno proves that swift Achilles can never catch up with a lumbering tortoise that has a head start. To make things more concrete, let's put some numbers on the problem. Imagine that Achilles runs at a foot a second, while the tortoise runs at half that speed. Imagine, too, that the tortoise starts off a foot ahead of Achilles.
Achilles speeds ahead, and in a mere second he has caught up to where the tortoise was. But by the time he reaches that point, the tortoise, which is also running, has moved ahead by half a foot. No matter. Achilles is faster, so in half a second, he makes up the half foot. But again, the tortoise has moved ahead, this time by a quarter foot. In a flashâa quarter secondâAchilles has made up the distance. But the tortoise lumbers ahead in that time by an eighth of a foot. Achilles runs and runs, but the tortoise scoots ahead each time; no matter how close Achilles gets to the tortoise, by the time he reaches the point where the tortoise was, the tortoise has moved. An eighth of a footâ¦a sixteenth of a footâ¦a thirty-second of a footâ¦smaller and smaller distances, but Achilles never catches up. The tortoise is always ahead (Figure 10).
Everybody knows that, in the real world, Achilles would quickly run past the tortoise, but Zeno's argument seemed to prove that Achilles could never catch up. The philosophers of his day were unable to refute the paradox. Even though they knew that the conclusion was wrong, they could never find a mistake in Zeno's mathematical proof. The philosophers' main weapon was logic, but logical deduction seemed useless against Zeno's argument. Each step along the way seemed airtight, and if all the steps are correct, how could the conclusion be wrong?
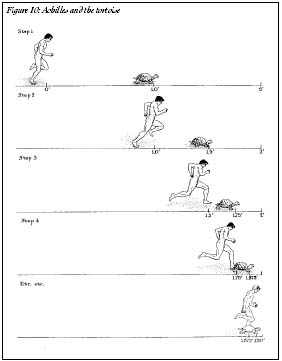
Figure 10: Achilles and the tortoise
The Greeks were stumped by the problem, but they did find the source of the trouble: infinity. It is the infinite that lies at the heart of Zeno's paradox: Zeno had taken continuous motion and divided it into an infinite number of tiny steps. Because there are an infinite number of steps, the Greeks assumed that the race would go on forever and ever, even though the steps get smaller and smaller. The race would never finish in finite timeâor so they thought. The ancients didn't have the equipment to deal with the infinite, but modern mathematicians have learned to handle it. The infinite must be approached very carefully, but it can be mastered, with the help of zero. Armed with 2,400 years' worth of extra mathematics, it is not hard for us to go back and find Zeno's Achilles' heel.
The Greeks did not have zero, but we do, and it is the key to solving Zeno's puzzle. It is sometimes possible to add infinite terms together to get a finite resultâbut to do so, the terms being added together must approach zero.
*
This is the case with Achilles and the tortoise. When you add up the distance that Achilles runs, you start with the number 1, then add ½, then add ¼, then add
1
/
8
, and so on, with the terms getting smaller and smaller, getting closer and closer to zero; each term is like a step along a journey where the destination is zero. However, since the Greeks rejected the number zero, they couldn't understand that this journey could ever have an end. To them, the numbers 1, ½, ¼,
1
/
8
,
1
/
16
, and so forth aren't approaching anything; the destination doesn't exist. Instead, the Greeks just saw the terms as simply getting smaller and smaller, meandering outside the realm of numbers.
Modern mathematicians know that the terms have a
limit;
the numbers 1, ½, ¼,
1
/
8
,
1
/
16
, and so forth are approaching zero as their limit. The journey has a destination. Once the journey has a destination, it is easy to ask how far away that destination is and how long it will take to get there. It is not that difficult to sum up the distances that Achilles runs: 1 + ½ + ¼ +
1
/
8
+
1
/
16
+â¦+ ½
n
+â¦. In the same way that the steps that Achilles takes get smaller and smaller, and closer and closer to zero, the sum of those steps gets closer and closer to 2. How do we know this? Well, let's start off with 2, and subtract the terms of the sum, one by one. We begin with 2 - 1, which is, of course, 1. Next, we subtract ½, leaving ½. Then remove the next term: subtract ¼, leaving ¼ behind. Subtracting
1
/
8
leaves
1
/
8
behind. We're back to our familiar sequence. We already know that 1, ½, ¼,
1
/
8
, and so forth has a limit of zero; thus, as we subtract the terms from 2, we have nothing left. The limit of the sum 1 + ½ + ¼ +
1
/
8
+
1
/
16
+â¦is 2 (Figure 11). Achilles runs 2 feet in catching up to the tortoise, even though he takes an infinite number of steps to do it. Better yet, look at the time it takes Achilles to overtake the tortoise: 1 + ½ + ¼ +
1
/
8
+
1
/
16
+â¦â2 seconds. Not only does Achilles take an infinite number of steps to run a finite distance, but he takes only 2 seconds to do it.
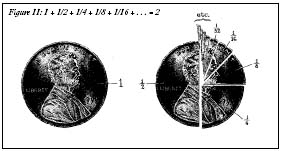
Figure 11: 1 + ½ + ¼ +
1
/
8
+
1
/
16
+â¦= 2
The Greeks couldn't do this neat little mathematical trick. They didn't have the concept of a limit because they didn't believe in zero. The terms in the infinite series didn't have a limit or a destination; they seemed to get smaller and smaller without any particular end in sight. As a result, the Greeks couldn't handle the infinite. They pondered the concept of the void but rejected zero as a number, and they toyed with the concept of the infinite but refused to allow infinityânumbers that are infinitely small and infinitely largeâanywhere near the realm of numbers. This is the biggest failure in Greek mathematics, and it is the only thing that kept them from discovering calculus.
Infinity, zero, and the concept of limits are all tied together in a bundle. Greek philosophers were unable to untie that bundle; therefore, they were ill-equipped to solve Zeno's puzzle. Yet Zeno's paradox was so powerful that the Greeks tried over and over to explain away his infinities. They were doomed to failure, unarmed with the proper concepts.
Zeno himself didn't have a proper solution to the paradox, nor did he seek one. The paradox suited his philosophy perfectly. He was a member of the Eleatic school of thought, whose founder, Parmenides, held that the underlying nature of the universe was changeless and immobile. Zeno's puzzles appear to have been in support of Parmenides' argument; in showing that change and motion were paradoxical, he hoped to convince people that everything is oneâand changeless. Zeno really did believe that motion was impossible, and his paradox was this theory's chief support.
There were other schools of thought. The atomists, for example, believed that the universe is made up of little particles called atoms, which are indivisible and eternal. Motion, according to the atomists, was the movement of these little particles. Of course, for these atoms to move, there has to be empty space for them to move into. After all, these little atoms had to move around somehow; if there were no such thing as a vacuum, the atoms would be constantly pressed against one another. Everything would be stuck in one position for eternity, unable to move. Thus, the atomic theory required that the universe be filled with emptinessâan infinite void. The atomists embraced the concept of the infinite vacuumâinfinity and zero wrapped into one. This was a shocking conclusion, but the indivisible kernels of matter in atomic theory got around the problem of Zeno's paradoxes. Because atoms are indivisible, there is a point beyond which things could not be divided. Zeno's hair-splitting doesn't go on ad infinitum. After a number of strides, Achilles would be taking tiny steps that can't get any smaller; eventually he would have to hurdle an atom that the tortoise doesn't. Achilles would finally catch up to the elusive turtle.
Another philosophy vied with the atomic theory, and instead of posing such bizarre concepts as the infinite vacuum, it turned the universe into a cozy nutshell. There was no infinity, no voidâjust beautiful spheres that surrounded the earth, which was naturally placed at the very center of the universe. This was the Aristotelian system, which was later refined by the Alexandrian astronomer Ptolemy. It became the dominant philosophy in the Western world. And by rejecting zero and infinity, Aristotle explained away Zeno's paradoxes.
Aristotle simply declared that mathematicians “do not need the infinite, or use it.” Though “potential” infinities could exist in the minds of mathematiciansâlike the concept of dividing lines into infinite piecesânobody could actually do it, so the infinite doesn't exist in reality. Achilles runs smoothly past the tortoise because the infinite points are simply a figment of Zeno's imagination, rather than a real-world construct. Aristotle just wished infinity away by stating that it is simply a construct of the human mind.
From that concept comes a startling revelation. Based upon the Pythagorean universe, the Aristotelian cosmos (and its later refinement by the astronomer Ptolemy) had the planets moving in crystalline orbs. However, since there is no infinity, there can't be an endless number of spheres; there must be a last one. This outermost sphere was a midnight blue globe encrusted with tiny glowing points of lightâthe stars. There was no such thing as “beyond” the outermost sphere; the universe ended abruptly with that outermost layer. The universe was contained in a nutshell, ensconced comfortably within the sphere of fixed stars; the cosmos was finite in extent, and entirely filled with matter. There was no infinite; there was no void. There was no infinity; there was no zero.
This line of reasoning had another consequenceâand this is why Aristotle's philosophy endured for so many years. His system proved the existence of God.
The heavenly spheres are slowly spinning in their places, making a music that suffuses the cosmos. But something must be causing that motion. The stationary earth cannot be the source of that motive power, so the innermost sphere must be moved by the next sphere out. That sphere, in turn, is moved by its larger neighbor, and on and on. However, there is no infinity; there are a finite number of spheres, and a finite number of things that are moving each other. Something must be the ultimate cause of motion. Something must be moving the sphere of fixed stars. This is the prime mover: God. When Christianity swept through the West, it became closely tied to the Aristotelian view of the universe and the proof of God's existence. Atomism became associated with atheism. Questioning the Aristotelian doctrine was tantamount to questioning God's existence.