Zero (22 page)
Authors: Charles Seife

Cantor generalized this trick. He said that two sets of numbers are the same size when one set of numbers can “sit” on top of another set of numbersâone to a customerâwith none left over. For instance, consider the set {1, 2, 3}. It is the same size as {2, 4, 6} because we can make a perfect seating pattern where all the numbers are “seated” and all the “seats” are occupied:
1 2 3
| | |
2 4 6
But it's not the same size as {2, 4, 6, 8}
1 2 3
| | | |
2 4 6 8
because 8 is an empty “seat.”
Things get really interesting when you get to infinite sets. Consider the set of whole numbers: {0, 1, 2, 3, 4, 5,â¦}. Obviously, this set is equal to itself; we can just have each number “sit” upon itself:
0 1 2 3 4 5â¦
| | | | | |
0 1 2 3 4 5â¦
There's no trick here. Every set is obviously equal to itself. But what happens when we start removing numbers from the set? For instance, what happens when we remove 0? Oddly enough, removing 0 doesn't change the size of the set at all. By rearranging the seating pattern slightly, we can ensure that everybody has a seat, and all the seats are still taken:
1 2 3 4 5 6â¦
| | | | | |
0 1 2 3 4 5â¦
The set is the same size, even though we've removed something from it. In fact, we can remove an infinite number of elements from the set of whole numbersâwe can delete the odd numbers, for exampleâand the size of the set remains unchanged. Everybody still has a seat, and every seat is filled:
0 2 4 6 8 10â¦
| | | | | |
0 1 2 3 4 5â¦
This is the definition of the infinite: it is something that can stay the same size even when you subtract from it.
The even numbers, the odd numbers, the whole numbers, the integersâall of these sets were the same size, a size that Cantor soon dubbed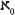 (aleph nought, named after the first letter of the Hebrew alphabet). Since these numbers are the same size as the counting numbers, any set of size
(aleph nought, named after the first letter of the Hebrew alphabet). Since these numbers are the same size as the counting numbers, any set of size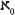 is called
is called
countable.
(Of course, you couldn't really count them unless you had an infinite amount of time on your hands.) Even the rational numbersâthe set of numbers that can be written as
a
/
b
for integers
a
and
b
âwere countable. By a clever way of assigning rational numbers to their proper seats, Cantor showed that the rationals were an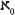 -sized set (see appendix D).
-sized set (see appendix D).
But as Pythagoras knew, the rationals aren't everything under the sun; both the rationals and irrationals make up the so-called real numbers. Cantor discovered that the set of real numbers is much, much bigger than the rationals. His proof was a very simple one.
Imagine that we've already got a perfect seating plan for the real numbers: every real number has a seat, and every seat is filled. That means we can make a list of seats, showing a seat's number along with the real number that is sitting in it. For instance, our list might look like the following:

The trick came when Cantor created a real number that was not on the list.
Look at the first digit of the first number on the list; in our example, it's a 3. If our new number were equal to the first number on the list, it would also have a first digit of 3âbut we can easily prevent that from happening. Let's just say that our new number has a first digit of 2. Since the first number on the list starts with a 3 and our new number starts with a 2, we know that the two numbers are different. (This is not strictly true. The number 0.300000â¦is equal to 0.2999999â¦, since there are two ways to write many rational numbers. But this is a minor point that is easily overcome. For the sake of clarity, we'll ignore that exception.)
On to the second number. How can we make sure that our new number is different from the second number on the list? Well, we've already determined the first digit in our new number, so we can't pull exactly the same trick, but we can do something just as good. The second number on the list has an 8 for its second digit. If our new number has a 7 for its second digit, we can ensure that our new number is not the same as the second number on the list; their second digits don't match, so they aren't the same thing. We do the same thing on down the list; look at the third digit of the third number and change it, look at the fourth digit on the fourth number and change it, and so on.

Yielding a new number, .27800â¦, that
is different from the first number (their first digits don't match),
is different from the second number (their second digits don't match),
is different from the third number (their third digits don't match),
is different from the fourth number (their fourth digits don't match), and so forth.
Â
Going down the diagonal in this way, we create a new number. This process ensures that it's different from all the other numbers on the list. If it is different from all the numbers on the list, it can't be on the listâbut we already assumed our list contains all real numbers; after all, it was a perfect seating list. This is a contradiction. The perfect seating list cannot exist.
The real numbers are a bigger infinity than the rational numbers. The term for this type of infinity was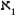 , the first
, the first
uncountable
infinity. (Technically, the term for the infinity of the real line was
C,
or the continuum infinity. For years mathematicians struggled to determine whether
C
was indeed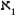 . In 1963 a mathematician, Paul Cohen, proved that this puzzle, the so-called continuum hypothesis, was neither provable nor disprovable, thanks to Gödel's incompleteness theorem. Today most mathematicians accept the continuum hypothesis as true, though some study
. In 1963 a mathematician, Paul Cohen, proved that this puzzle, the so-called continuum hypothesis, was neither provable nor disprovable, thanks to Gödel's incompleteness theorem. Today most mathematicians accept the continuum hypothesis as true, though some study
non-Cantorian transfinite numbers
where the continuum hypothesis is taken to be false.) In Cantor's mind there were an infinite number of infinitiesâthe transfinite numbersâeach nested in the other.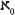 is smaller than
is smaller than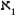 , which is smaller than
, which is smaller than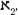 , which is smaller than
, which is smaller than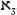 , and so forth. At the top of the chain sits the ultimate infinity that engulfs all other infinities: God, the infinity that defies all comprehension.
, and so forth. At the top of the chain sits the ultimate infinity that engulfs all other infinities: God, the infinity that defies all comprehension.