Zero (19 page)
Authors: Charles Seife

Nobody could explain how those infinitesimals disappeared when squared; they just accepted the fact because making them vanish at the right time gave the correct answer. Nobody worried about dividing by zero when conveniently ignoring the rules of mathematics explained everything from the fall of an apple to the orbits of the planets in the sky. Though it gave the right answer, using calculus was as much an act of faith as declaring a belief in God.
The End of Mysticism
A quantity is something or nothing; if it is something, it has not yet vanished; if it is nothing, it has literally vanished. The supposition that there is an intermediate state between these two is a chimera.
âJ
EAN
L
E
R
OND D
'A
LEMBERT
In the shadow of the French Revolution, the mystical was driven out of calculus.
Despite calculus's shaky foundations, by the end of the eighteenth century, mathematicians all over Europe were having stunning successes with the new tool. Colin Maclaurin and Brook Taylor, perhaps the best British mathematicians in the era of isolation from the Continent, discovered how to use calculus to rewrite functions in a totally different form. For instance, after using some tricks in calculus, mathematicians realized that the function 1/(1 â
x
) can be written as
1 +
x
+
x
2
+
x
3
+
x
4
+
x
5
+â¦
Though the two expressions look dramatically different, they are (with some caveats) exactly the same.
Those caveats, which stem from the properties of zero and infinity, can become very important, however. The Swiss mathematician Leonhard Euler, inspired by calculus's easy manipulation of zeros and infinities, used similar reasoning as Taylor and Maclaurin and “proved” that the sum
â¦1/
x
3
+ 1/
x
2
+ 1/
x
+ 1 +
x
+
x
2
+
x
3
â¦
equals zero. (To convince yourself that something fishy is going on, plug in the number 1 for
x
and see what happens.) Euler was an excellent mathematicianâin fact, he was one of the most prolific and influential in historyâbut in this case the careless manipulation of zero and infinity led him astray.
It was a foundling who finally tamed the zeros and infinities in calculus and rid mathematics of its mysticism. In 1717 an infant was found on the steps of the church of Saint Jean Baptiste le Rond in Paris. In memory of that occasion, the child was named Jean Le Rond, and he eventually took the surname d'Alembert. Though he was raised by an impoverished working-class coupleâhis foster father was a glazierâit turns out that his birth father was a general and his mother was an aristocrat.
D'Alembert is best known for his collaboration on the famed
Encyclopédie
of human knowledgeâa 20-year effort with coauthor Denis Diderot. But d'Alembert was more than an encyclopedist. It was d'Alembert who realized that it was important to consider the journey as well as the destination. He was the one who hatched the idea of
limit
and solved calculus's problems with zeros.
Once again, let us consider the story of Achilles and the tortoise, which is an infinite sum of steps that get closer and closer to zero. Manipulating an infinite sumâwhether it is in the Achilles problem or in finding the area underneath a curve or finding an alternate form for a mathematical functionâcaused mathematicians to come up with contradictory results.
D'Alembert realized that the Achilles problem vanishes if you consider the
limit
of the race. In our example on page 41, at every step the tortoise and Achilles get closer and closer to the two-foot mark. No step takes them farther away or even keeps them at the same distance; each moment brings them closer to that mark. Thus, the limit of that raceâits ultimate destinationâis at the two-foot mark. This is where Achilles passes the tortoise.
But how do you prove that two feet is actually the limit of the race? I ask you to challenge me. Give me a tiny distance, no matter how small, and I will tell you when both Achilles and the tortoise are less than that tiny distance away from the limit.
As an example, let's say that you challenge me with a distance of one-thousandth of a foot. Well, a few calculations later, I would tell you that after the 11th step, Achilles is 977 millionths of a foot away from the two-foot mark, while the tortoise is half that distance away; I have met your challenge with 23 millionths of a foot to spare. What if you challenged me with a distance of one-billionth of a foot? After 31 steps, Achilles is 931 trillionths of a foot away from the targetâ69 trillionths closer than you neededâwhile the tortoise, again, is half that distance away. No matter how you challenge me, I can meet that challenge by telling you a time when Achilles is closer to the mark than you require. This shows that, indeed, Achilles is getting arbitrarily close to the two-foot mark as the race progresses: two feet is the limit of the race.
Now, instead of thinking of the race as a sum of infinite parts, think of it as a limit of finite sub-races. For instance, in the first race Achilles runs to the one-foot mark. Achilles has run
1
1 foot in all. In the next race Achilles does the first two partsâfirst running 1 foot, and then a half foot. In total, Achilles has run
1 + ½
1.5 feet in all. The third race takes him as far as
1 + ½ + ¼
1.75 feet, all told. Each of these sub-races is finite and well-defined; we never encounter an infinity.
What d'Alembert did informallyâand what the Frenchman Augustin Cauchy, the Czech Bernhard Bolzano, and the German Karl Weierstrass would later formalizeâwas to rewrite the infinite sum
1 + ½ + ¼ +
1
/
8
+â¦+ ½
n
+â¦
as the expression
limit (as
n
goes to ?) of 1 + ½ + ¼ +
1
/
8
+â¦+ ½
n
Â
It's a very subtle change in notation, but it makes all the difference in the world.
When you have an infinity in an expression, or when you divide by zero, all the mathematical operationsâeven those as simple as addition, subtraction, multiplication, and divisionâgo out the window. Nothing makes sense any longer. So when you deal with an infinite number of terms in a series, even the + sign doesn't seem so straightforward. That is why the infinite sum of +1 and -1 we saw at the beginning of the chapter seems to equal 0 and 1 at the same time.
However, by putting this limit sign in front of a series, you separate the process from the goal. In this way you avoid manipulating infinities and zeros. Just as Achilles' sub-races are each finite, each
partial sum
in a limit is finite. You can add them, divide them, square them; you can do whatever you want. The rules of mathematics still work, since everything is finite. Then, after all your manipulations are complete, you take the limit: you extrapolate and figure out where the expression is headed.
Sometimes that limit doesn't exist. For instance, the infinite sum of +1 and -1 does not have a limit. The value of the partial sums flips back and forth between 1 and 0; it's not really heading to a predictable destination. But with Achilles' race, the partial sums go from 1 to 1.5 to 1.75 to 1.875 to 1.9375 and so forth; they get closer and closer to two. The sums have a destinationâa limit.
The same thing goes for taking the derivative. Instead of dividing by zero as Newton and Leibniz did, modern mathematicians divide by a number that they let approach zero. They do the divisionâperfectly legally, since there are no zerosâthen they take the limit. The dirty tricks of making squared infinitesimals disappear and then dividing by zero to get a derivative were no longer necessary (see appendix C).
This logic may seem like splitting hairs, like an argument as mystical as Newton's “ghosts,” but in reality it's not. It satisfies the mathematician's strict requirement of logical rigor. There is a very firm, consistent basis for the concept of limits. Indeed, you can even dispense with the “I challenge you” argument entirely, as there are other ways of defining a limit, such as calling it the convergence of two numbers, the
lim sup
and
lim inf.
(I have a wonderful proof of this, but alas, this book is too small to contain it.) Since limits are logically airtight, by defining a derivative in terms of limits, it becomes airtight as wellâand puts calculus on a solid foundation.
No longer was it necessary to divide by zeros. Mysticism vanished from the realm of mathematics and logic ruled once more. The peace lasted until the Reign of Terror.
6
Infinity's Twin
[THE INFINITE NATURE OF ZERO]
God made integers; all else is the work of man.
âL
EOPOLD
K
RONECKER
Z
ero and infinity always looked suspiciously alike. Multiply zero by anything and you get zero. Multiply infinity by anything and you get infinity. Dividing a number by zero yields infinity; dividing a number by infinity yields zero. Adding zero to a number leaves the number unchanged. Adding a number to infinity leaves infinity unchanged.
These similarities were obvious since the Renaissance, but mathematicians had to wait until the end of the French Revolution before they finally unraveled zero's big secret.
Zero and infinity are two sides of the same coinâequal and opposite, yin and yang, equally powerful adversaries at either end of the realm of numbers. The troublesome nature of zero lies with the strange powers of the infinite, and it is possible to understand the infinite by studying zero. To learn this, mathematicians had to venture into the world of the imaginary, a bizarre world where circles are lines, lines are circles, and infinity and zero sit on opposite poles.
The Imaginary
â¦a fine and wonderful refuge of the divine spiritâalmost an amphibian between being and non-being.
âG
OTTFRIED
W
ILHELM
L
EIBNIZ
Zero is not the only number that was rejected by mathematicians for centuries. Just as zero suffered from Greek prejudice, other numbers were ignored as well, numbers that made no geometric sense. One of these numbers,
i,
held the key to zero's strange properties.
Algebra presented another way of looking at numbers, entirely divorced from the Greek geometric ideas. Instead of trying to measure the area inside a parabola as the Greeks did, early algebraists sought to find the solutions to equations that encode relationships between different numbers. For instance, the simple equation 4
x
- 12 = 0 describes how an unknown number
x
is related to 4, 12, and 0. The task of the algebra student is to figure out what number
x
is. In this case
x
is 3. Substitute 3 for
x
in the above equation and you will quickly see that the equation is satisfied; 3 is a solution for the equation 4
x
- 12 = 0. In other words, 3 is a
zero
or a
root
of the expression 4
x
- 12.
When you start stringing symbols together to get equations, you can wind up with something unexpected. For instance, take the above equation and change the - sign into a + sign. This leaves us with a very innocent-looking equation, 4
x
+ 12 = 0, but the solution to that equation is now - 3, a negative number.
Just as Indian mathematicians accepted zero while Europeans rejected it for centuries, the East embraced negative numbers while the West tried to ignore them. As late as the seventeenth century, Descartes refused to accept negative numbers as roots of equations. He called them “false roots,” which explains why he never extended his coordinate system to the negative numbers. Descartes was a late holdover, a victim of his success in marrying algebra to geometry. Negative numbers had long been useful to algebraistsâeven Western algebraists. Negative numbers came up all the time in solving equations, such as quadratic equations.
A
linear
equation like 4
x
- 12 = 0 is extremely simple to solve, and such problems didn't entertain algebraists for very long. So they soon turned to more difficult problems: quadratic equationsâequations that begin with an
x
2
term, like
x
2
- 1 = 0. Quadratic equations are more complicated than regular equations; for one thing, they can have two different roots. For instance,
x
2
- 1 = 0 has two solutions: 1 and -1. (Substitute -1 or 1 for
x
in the equation and you'll see what happens.) Either one of those solutions works; as it turns out, the expression
x
2
- 1
splits
into (
x
- 1)(
x
+ 1), making it easy to see that if
x
is 1 or -1, the expression goes to zero.
Though quadratic equations are more complicated than linear equations, there is a simple way to figure out what the roots of a quadratic equation are. It's the famous quadratic formula, which is the crowning achievement of high-school algebra class. The formula for finding the roots of a quadratic equation
ax
2
+
bx
+
c
= 0 is: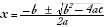 . The + sign gives us one root, while the - sign gives us the other. The quadratic formula has been known for centuries; the ninth-century mathematician al-Khowarizmi knew how to solve almost every quadratic equation, though he didn't seem to consider negative numbers as roots. Not long after that, algebraists learned to accept negative numbers as valid solutions to equations. Imaginary numbers, though, were a little different.
. The + sign gives us one root, while the - sign gives us the other. The quadratic formula has been known for centuries; the ninth-century mathematician al-Khowarizmi knew how to solve almost every quadratic equation, though he didn't seem to consider negative numbers as roots. Not long after that, algebraists learned to accept negative numbers as valid solutions to equations. Imaginary numbers, though, were a little different.
Imaginary numbers never appeared in linear equations, but they began to crop up in quadratic ones. Consider the equation
x
2
+ 1 = 0. No number seems to solve the equation; plugging in â1, 3, â750, 235.23, or any other positive or negative number you could think of doesn't yield the correct answer. The expression simply will not split. Worse yet, when you try to apply the quadratic equation, you get two silly-sounding answers:

These expressions don't seem to make any sense. The Indian mathematician Bhaskara wrote in the twelfth century that “there is no square root of a negative number, for a negative number is not a square.” What Bhaskara and others realized was that when you square a positive number, you get a positive number back; 2 times 2 equals 4, for instance. When you square a negative number, you still get a positive number: â2 times â2 also equals 4. When you square zero, you get zero. Positive numbers, negative numbers, and zero all give you nonnegative squares, and those three possibilities cover the whole number line. This means that there is no number on the number line that gives you a negative number when you square it. The square root of a negative number seemed like a ridiculous concept.
Descartes thought that these numbers were even worse than negative numbers; he came up with a scornful name for the square roots of negatives:
imaginary numbers.
The name stuck, and eventually, the symbol for the square root of â1 became
i.
Algebraists loved
i
. Almost everyone else hated it. It was wonderful for solving polynomialsâexpressions like
x
3
+ 3
x
+ 1 that have
x
raised to various powers. In fact, once you allow
i
into the realm of numbers, every polynomial becomes solvable:
x
2
+ 1 suddenly splits into (
x
-
i
)(
x
+
i
)âthe roots of the equation are +
i
and -
i.
Cubic expressions like
x
3
-
x
2
+
x
- 1 split three ways, such as (
x
- 1)(
x
+
i
)(
x
-
i
). Quartic expressionsâones with a leading
x
4
termâalways split into four terms, and quinticsâones with a leading
x
5
termâsplit five ways. All polynomials of degree
n
âthose that have a leading term of
x
n
âsplit into
n
distinct terms. This is the
fundamental theorem of algebra.
As early as the sixteenth century, mathematicians were using numbers with
i
includedâthe so-called
complex numbers
âto solve cubic and quartic polynomials. And while many mathematicians saw the complex numbers as a convenient fiction, others saw God.
Leibniz thought that
i
was a bizarre mix between existence and nonexistence, something like a cross between 1 (God) and 0 (Void) in his binary scheme. Leibniz likened
i
to the Holy Spirit: both have an ethereal and barely substantial existence. But even Leibniz didn't realize that
i
would finally reveal the relationship between zero and infinity. It would take two important developments in mathematics before the true link was uncovered.
Point and Counterpoint
One will then see the simplicity with which these concepts lead to properties already known and to an infinity of others which ordinary geometry does not seem to touch easily.
âJ
EAN-
V
ICTOR
P
ONCELET
The first developmentâprojective geometryâwas born in the turmoil of war. In the 1700s, France, England, Austria, Prussia, Spain, the Netherlands, and other countries were vying for power. Alliances formed and broke over and over again; new territorial disputes erupted over colonies, and countries struggled to dominate trade to and from the New World. France, England, and other countries skirmished throughout the first half of the eighteenth century, and roughly a quarter century after Newton died, a full-scale war erupted. France, Austria, Spain, and Russia fought England and Prussia for nine years.
In 1763 the French capitulated and the Seven Years' War was over. (Two years of fighting occurred before war was officially declared.) The victory made England the preeminent power in the world, but it came at a great cost. Both France and England were exhausted and in debtâand they would both suffer the consequences: revolutions. A little more than a decade after the end of the Seven Years' War, the American Revolution began; the revolt would strip England of its richest colony. In 1789, just as George Washington was sworn into office in the newly founded United States, the French Revolution began. Four years later the revolutionaries removed the French king's head.
A mathematician, Gaspard Monge, signed the revolutionary government's record of the king's execution. Monge was a consummate geometer, specializing in three-dimensional geometry. He was responsible for the way architects and engineers draw buildings and machines: they project the design onto a vertical plane and a horizontal plane, preserving all the information needed to reconstruct the object. Monge's work was so important to the military that much of it was made into a state secret by the revolutionary government and by the Napoleonic government that succeeded it soon afterward.
Jean-Victor Poncelet was a student of Monge's who learned about three-dimensional geometry as he trained to become an engineer for Napoleon's army. Unluckily for Poncelet, he entered the army just as Napoleon set off for Moscow in 1812.