Zero (14 page)
Authors: Charles Seife

5
Infinite Zeros and Infidel Mathematicians
[ZERO AND THE SCIENTIFIC REVOLUTION]
With the introduction ofâ¦the infinitely small and infinitely large, mathematics, usually so strictly ethical, fell from graceâ¦. The virgin state of absolute validity and irrefutable proof of everything mathematical was gone forever; the realm of controversy was inaugurated, and we have reached the point where most people differentiate and integrate not because they understand what they are doing but from pure faith, because up to now it has always come out right.
âF
RIEDRICH
E
NGELS
,
A
NTI-
D
UHRING
Z
ero and infinity had destroyed the Arisotelian philosophy; the void and the infinite cosmos had eliminated the nutshell universe and the idea of nature's abhorrence of the vacuum. The ancient wisdom was discarded, and scientists began to divine the laws that governed the workings of nature. However, there was a problem with the scientific revolution: zero.
Deep within the scientific world's powerful new toolâcalculusâwas a paradox. The inventors of calculus, Isaac Newton and Gottfried Wilhelm Leibniz, created the most powerful mathematical method ever by dividing by zero and adding an infinite number of zeros together. Both acts were as illogical as adding 1 + 1 to get 3. Calculus, at its core, defied the logic of mathematics. Accepting it was a leap of faith. Scientists took that leap, for calculus is the language of nature. To understand that language completely, science had to conquer the infinite zeros.
The Infinite Zeros
When, after a thousand-year stupor, European thought shook off the effect of the sleeping powders so skilfully administered by the Christian Fathers, the problem of infinity was one of the first to be revived.
âT
OBIAS
D
ANZIG
,
N
UMBER
: T
HE
L
ANGUAGE OF
S
CIENCE
Zeno's curse hung over mathematics for two millennia. Achilles seemed doomed to chase the tortoise forever, never catching up. Infinity lurked in Zeno's simple riddle. The Greeks were stumped by Achilles' infinite steps. They never considered adding infinite parts together even though Achilles' strides approach zero size; the Greeks could hardly add steps of zero size together without the concept of zero. However, once the West embraced zero, mathematicians began to tame the infinite and ended Achilles' race.
Even though Zeno's sequence has infinite parts, we can add all of the steps together and still stay within the realm of the finite: 1 + ½ + ¼ +
1
/
8
+
1
/
16
+â¦= 2. The first person to do this sort of trickâadding infinite terms to get a finite resultâwas the fourteenth-century British logician Richard Suiseth. Suiseth took an infinite sequence of numbers: ¼,
2
/
4
,
3
/
8
,
4
/
16
,â¦,
n
/
2
n
,â¦, and added them all together, yielding two. After all, the numbers in the sequence get closer and closer to zero; naively, one would guess that this would ensure that the sum remains finite. Alas, the infinite is not quite that simple.
At about the same time Suiseth was writing, Nicholas Oresme, a French mathematician, tried his hand at adding together another infinite sequence of numbersâthe so-called harmonic series:
½ +
1
/
3
+ ¼ +
1
/
5
+
1
/
6
+â¦
Like the Zeno sequence and Suiseth's sequence, all the terms get closer and closer to zero. However, when Oresme tried to sum the terms in the sequence, he realized that the sums got larger and larger and larger. Even though the individual terms go to zero, the sum goes off to infinity. Oresme showed this by clumping the terms together: ½ + (
1
/
3
+ ¼) + (
1
/
5
+
1
/
6
+
1
/
7
+
1
/
8
) +â¦. The first group clearly equals ½; the second group is greater than (¼ + ¼), or ½. The third group is greater than (
1
/
8
+
1
/
8
+
1
/
8
+
1
/
8
), or ½. And so forth. You keep adding ½ after ½ after ½, and the sum gets bigger and bigger, and off to infinity. Even though the terms themselves go to zero, they don't approach zero fast enough. An infinite sum of numbers can be infinite, even if the numbers themselves approach zero. Yet this isn't the strangest aspect of infinite sums. Zero itself is not immune to the bizarre nature of infinity.
Consider the following series: 1 â 1 + 1 â 1 + 1 â 1 + 1 â 1 + 1 ââ¦. It's not so hard to show that this series sums to zero. After all,
(1 â 1) + (1 â 1) + (1 â 1) + (1 â 1) + (1 â 1) + (1 â 1) +â¦
is the same thing as
0 + 0 + 0 + 0 + 0 + 0 +â¦
which clearly sums to zero. But beware! Group the series in a different way:
1 + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1) + (-1 + 1) +â¦
is the same thing as
1 + 0 + 0 + 0 + 0 + 0 +â¦
which clearly sums to one. The same infinite sum of zeros can equal 0 and 1 at the same time. An Italian priest, Father Guido Grandi, even used this series to prove that God could create the universe (1) out of nothing (0). In fact, the sequence can be set to equal anything at all. To make the sum equal 5, start with 5s and -5s instead of 1s and -1s, and we can show that 0 + 0 + 0 + 0 +â¦equals 5.
Adding infinite things to each other can yield bizarre and contradictory results. Sometimes, when the terms go to zero, the sum is finite, a nice, normal number like 2 or 53. Other times the sum goes off to infinity. And an infinite sum of zeros can equal anything at allâand everything at the same time. Something very bizarre was going on; nobody knew quite how to handle the infinite.
Luckily the physical world made a little more sense than the mathematical one. Adding infinite things to each other seems to work out most of the time, so long as you are dealing with something in real life, like finding the volume of a barrel of wine. And 1612 was a banner year for wine.
Johannes Keplerâthe man who figured out that planets move in ellipsesâspent that year gazing into wine barrels, since he realized that the methods that vintners and coopers used to estimate the size of barrels were extremely crude. To help the wine merchants out, Kepler chopped up the barrelsâin his mindâinto an infinite number of infinitely tiny pieces, and then added them back together again to yield their volumes. This may seem a backward way of going about measuring barrels, but it was a brilliant idea.
To make the problem a bit simpler, let us consider a two-dimensional object rather than a three-dimensional oneâa triangle. The triangle in Figure 23 has a height of 8 and a base of 8; since the area of a triangle is half the base times the height, the area is 32.
Now imagine trying to estimate the size of the triangle by inscribing little rectangles inside the triangle. For a first try, we get an area of 16, quite short of the actual value of 32. The second try is a bit better; with three rectangles, we get a value of 24. Closer, but still not there yet. The third try gives us 28âcloser still. As you can see, making smaller and smaller rectanglesâwhose widths, denoted by the symbol ?
x,
go to zeroâmakes the value closer and closer to 32, the true value for the area of the triangle. (The sum of these rectangles is equal to ?
f
(
x
)?
x
where the Greek ? represents the sum over an appropriate range and
f
(
x
) is the equation of the curve that the rectangles strike. In modern notation, as ?
x
goes to zero, we replace the ? with a new symbol, , and ?
, and ?
x
with dx, turning the equation into f
f
(
x
) dx, which is the integral.)
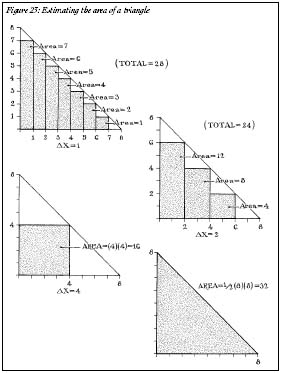
Figure 23: Estimating the area of a triangle
In one of Kepler's lesser-known works,
Volume-Measurement of Barrels,
he does this in three dimensions, slicing barrels into planes and summing the planes together. Kepler, at least, wasn't afraid of a glaring problem: as ?
x
goes to zero, the sum becomes equivalent to adding an infinite number of zeros togetherâa result that makes no sense. Kepler ignored the problem; though adding infinite zeros together was gibberish from a logical point of view, the answer it yielded was the right one.
Kepler was not the only prominent scientist who sliced objects infinitely thin. Galileo, too, pondered infinity and these infinitely small slices of area. These two ideas transcend our finite understanding, he wrote, “the former on account of their magnitude, the latter because of their smallness.” Yet despite the deep mystery of the infinite zeros, Galileo sensed their power. “Imagine what they are when combined,” he wondered. Galileo's student Bonaventura Cavalieri would provide part of the answer.
Instead of barrels, Cavalieri cut up geometric objects. To Cavalieri, every area, like that of the triangle, is made up of an infinite number of zero-width lines, and a volume is made up of an infinite number of zero-height planes. These
indivisible
lines and planes are like atoms of area and volume; they can't be divided any further. Just as Kepler measured the volumes of barrels with his thin slices, Cavalieri added up an infinite number of these indivisible zeros to figure out the area or the volume of a geometric object.
For geometers, Cavalieri's statement was troublesome indeed; adding infinite zero-area lines could not yield a two-dimensional triangle, nor could infinite zero-volume planes add up to a three-dimensional structure. It was the same problem: infinite zeros make no logical sense. However, Cavalieri's method always gave the right answer. Mathematicians ignored the logical and philosophical troubles with adding infinite zerosâespecially since indivisibles or
infinitesimals,
as they came to be called, finally solved a long-standing puzzle: the problem of the tangent.
A tangent is a line that just kisses a curve. For any point along a smooth curve that flows through space, there is a line that just grazes the curve, touching at exactly one point. This is the tangent, and mathematicians realized that it is extremely important in studying motion. For instance, imagine swinging a ball on a string around your head. It's traveling in a circle. However, if you suddenly cut the string, the ball will fly off along that tangent line; in the same way, a baseball pitcher's arm travels in an arc as he throws, but as soon as he lets go, the ball flies off on the tangent (Figure 24). As another example, if you want to find out where a ball will come to rest at the bottom of a hill, you look for a point where the tangent line is horizontal. The steepness of the tangent lineâits
slope
âhas some important properties in physics: for instance, if you've got a curve that represents the position of, say, a bicycle, then the slope of the tangent line to that curve at any given point tells you how fast that bicycle is going when it reaches that spot.