Zero (15 page)
Authors: Charles Seife


Figure 24: Flying off at a tangent
For this reason, several seventeenth-century mathematiciansâlike Evangelista Torricelli, René Descartes, the Frenchman Pierre de Fermat (famous for his last theorem), and the Englishman Isaac Barrowâcreated different methods for calculating the tangent line to any given point on a curve. However, like Cavalieri, all of them came up against the infinitesimal.
To draw a tangent line at any given point, it's best to make a guess. Choose another point nearby and connect the two. The line you get isn't exactly the tangent line, but if the curve isn't too bumpy, the two lines will be pretty close. As you reduce the distance between the points, the guess gets closer to the tangent line (Figure 25). When your points are zero distance away from each other, your approximation is perfect: you have found the tangent. Of course, there's a problem.
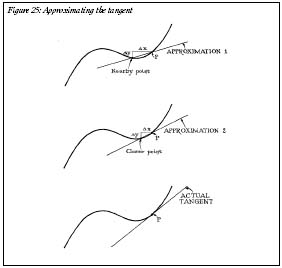
Figure 25: Approximating the tangent
The most important property of a line is its slope, and to measure this, mathematicians look at how high a line rises in a certain amount of distance. As an example, imagine you are driving east on a hill; for every mile east you drive, you gain half a mile in altitude. The slope of the hill is simply the heightâhalf a mileâover the horizontal distance you have drivenâone mile. Mathematicians say that the slope of the hill is ½. The same thing is true for lines; to measure the slope of a line, you look at how much the line rises (which mathematicians denote by the symbol ?
y
) in a given horizontal distance (which is denoted by ?
x
). The slope of the line is ?
y
/?
x.
When you try to calculate the slope of a tangent line, zero wrecks your approximation process. As your approximations of the tangent lines get better and better, the points on the curve you use to create the approximations get closer together. This means that the difference in height, ?
y,
goes to zero, as does the horizontal distance between the points, ?
x.
As your tangent approximations get better and better, ?
y
/?
x
approaches 0/0. Zero divided by zero can equal any number in the universe. Does the slope of the tangent line have any meaning?
Every time mathematicians tried to deal with the infinite or with zero, they encountered trouble with illogic. To figure out the volume of a barrel or the area under a parabola, mathematicians added infinite zeros together; to find out the tangent of a curve, they divided zero by itself. Zero and infinity made the simple acts of taking tangents and finding areas appear to be self-contradictory. These troubles would have ended as an interesting footnote but for one thing: these infinities and zeros are the key to understanding nature.
Zero and the Mystical Calculus
If we lift the veil and look underneathâ¦we shall discover much emptiness, darkness, and confusion; nay, if I mistake not, direct impossibilities and contradictionsâ¦. They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?
âB
ISHOP
B
ERKELEY
,
T
HE
A
NALYST
The tangent problem and the area problem both ran afoul of the same difficulties with infinities and zeros. It's no wonder, because the tangent problem and the area problem are actually the same thing. They are both aspects of calculus, a scientific tool far more powerful than anything ever seen before. The telescope, for instance, had given scientists the ability to find moons and stars that had never been observed before. Calculus, on the other hand, gave scientists a way to express the laws that govern the motion of the celestial bodiesâand laws that would eventually tell scientists how those moons and stars had formed. Calculus was the very language of nature, yet its very fabric was infused with zeros and infinities that threatened to destroy the new tool.
The first discoverer of calculus nearly died before he ever took a breath. Born prematurely on Christmas Day in 1642, Isaac Newton squirmed into the world, so small that he was able to fit into a quart pot. His father, a farmer, had died two months earlier.
Despite a traumatic childhood
*
and a mother who wanted him to become a farmer, Newton enrolled in Cambridge in the 1660sâand flourished. Within a few years he developed a systematic method of solving the tangent problem; he could figure out the tangent to any smooth curve at any point. This process, the first half of calculus, is now known as differentiation; however, Newton's method of differentiation doesn't look very much like the one we use today.
Newton's style of differentiation was based upon
fluxions
âthe flowsâof mathematical expressions that he called
fluents.
As an example of Newton's fluxions, take the equation
y = x
2
+ x + 1
In this equation, the fluents are
y
and
x;
Newton supposed that
y
and
x
are changing, or flowing, as time progresses. Their rates of changeâtheir fluxionsâare denoted by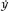 and
and respectively.
respectively.
Newton's method of differentiation was based on a notational trick: he let the fluxions change, but he only let them change infinitesimally. Essentially, he gave them no time to flow. In Newton's notation,
y
would change in that instant to (
y
+
o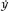 ) while
) while
x
changes to (
x
+
o ). (The letter
). (The letter
o
represented the amount of time that had passed; it was almost a zero, but not quite, as we shall see.) The equation then becomes
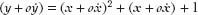
Multiplying out the (
x
+
o )
)
2
term gives us