Zero (12 page)
Authors: Charles Seife

Figure 19: Epicycles, retrograde motion, and heliocentrism

The Catholic Church had to strike back. Though it had been experimenting with other philosophies for several centuries, when threatened with schism it turned orthodox once again. It fell back upon its orthodox teachingsâthe Aristotelian-based philosophies of scholars like Saint Augustine and Boethius, as well as Aristotle's proof of God. No longer could cardinals and clerics question the ancient doctrines. Zero was a heretic. The nutshell universe had to be accepted; the void and the infinite must be rejected. One of the key groups that spread these teachings was founded in the 1530s: the Jesuit order, a collection of highly trained intellectuals well suited to attack Protestantism. The church had other tools to fight heresy as well; the Spanish Inquisition started burning Protestants in 1543, the same year Copernicus died and the same year that Pope Paul III issued the Index of forbidden books. The Counter-Reformation was the church's attempt to rebuild the old order by crushing the new ideas. An idea embraced by Bishop Ãtienne Tempier in the thirteenth century and Cardinal Nicholas of Cusa in the fifteenth century could mean a death sentence in the sixteenth century.
This is what happened to the unfortunate Giordano Bruno. In the 1580s, Bruno, a former Dominican cleric, published
On the Infinite Universe and Worlds,
where he suggested, like Nicholas of Cusa, that the earth was not the center of the universe and that there were infinite worlds like our own. In 1600 he was burned at the stake. In 1616 the famous Galileo Galilei, another Copernican, was ordered by the church to cease his scientific investigations. The same year, Copernicus's
De Revolutionibus
was placed on the Index of forbidden books. An attack on Aristotle was considered an attack upon the church.
Despite the church's Counter-Reformation, the new philosophy wasn't easily destroyed. It got stronger as time went on, thanks to the investigations of Copernicus's successors. In the beginning of the seventeenth century, another astrologer-monk, Johannes Kepler, refined Copernicus's theory, making it even more accurate than the Ptolemaic system. Instead of moving in circles, the planets, including Earth, moved in ellipses around the sun. This explained the motion of the planets in the heavens with incredible accuracy; no longer could astronomers object that the heliocentric system was inferior to the geocentric one. Kepler's model was simpler than Ptolemy's, and it was more accurate. Despite the church's objections, Kepler's heliocentric system would prevail eventually, because Kepler was right and Aristotle was wrong.
The church attempted to patch the holes in the old way of thought, but Aristotle, the geocentric world, and the feudal way of life were all mortally wounded. Everything that philosophers had taken for granted for millennia was called into doubt. The Aristotelian system could not be trusted, and at the same time it could not be rejected. What, then, could be taken for granted? Literally nothing.
Zero and the Void
I am in a sense something intermediate between God and nought.
âR
ENÃ
D
ESCARTES
,
D
ISCOURSE ON
M
ETHOD
Zero and the infinite were at the very center of the philosophical war taking place during the sixteenth and seventeenth centuries. The void had weakened Aristotle's philosophy, and the idea of an infinitely large cosmos helped shatter the nutshell universe. The earth could not be at the center of God's creation. As the papacy lost its hold on its flock, the Catholic Church tried to reject zero and the void more strongly than ever, yet zero had already taken root. Even the most devout intellectualsâthe Jesuitsâwere torn between the old, Aristotelian ways and the new philosophies that included zero and the void, infinity and the infinite.
René Descartes was trained as a Jesuit, and he, too, was torn between the old and the new. He rejected the void but put it at the center of his world. Born in 1596 in the middle of France, Descartes would bring zero to the center of the number line, and he would seek a proof of God in the void and the infinite. Yet Descartes could not reject Aristotle entirely; he was so afraid of the void that he denied its existence.
Like Pythagoras, Descartes was a mathematician-philosopher; perhaps his most lasting legacy was a mathematical inventionâwhat we now call Cartesian coordinates. Anyone who has taken geometry in high school has seen them: they are the sets of numbers in parentheses that represent a point in space. For instance, the symbol (4, 2) represents a point four units to the right and two units upward. But to the right and upward of what? The Origin. Zero (Figure 20).
Descartes realized that he could not start his two reference lines, or axes, with the number 1. That would lead to an error like the one Bede encountered when revamping the calendar. However, unlike Bede, he lived in a Europe where Arabic numerals were common, so he started counting with zero. At the very center of the coordinate systemâwhere the two axes crossâsits a zero. The origin, the point (0, 0), is the foundation of the Cartesian system of coordinates. (Descartes's notation was slightly different from what we use today. For one thing, he didn't extend his coordinate system to the negative numbers, though his colleagues would soon do that for him.)
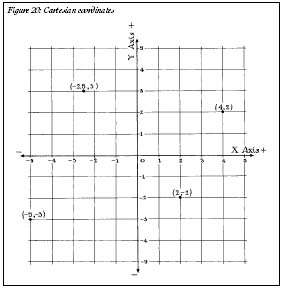
Figure 20: Cartesian coordinates
Descartes quickly realized how powerful his coordinate system was. He used it to turn figures and shapes into equations and numbers; with Cartesian coordinates every geometric objectâsquares, triangles, wavy linesâcould be represented by an equation, a mathematical relationship. For example, a circle at the origin can be represented by the set of all points where
x
2
+
y
2
â 1 = 0. A parabola might be
y
â
x
2
= 0. Descartes unified numbers and shapes. No longer were the Western art of geometry and the Eastern art of algebra separate domains. They were the same thing, as every shape could simply be expressed as an equation of the form
f
(
x, y
) = 0 (Figure 21). Zero was at the center of the coordinate system, and zero was implicit in each geometric shape.
To Descartes, zero was also implicit in God's domain, as was the infinite. Since the old Aristotelian doctrine was crumbling, Descartes, true to his Jesuit training, tried to use nought and infinity to replace the old proof of God's existence.
Like the ancients, Descartes assumed that nothing, not even knowledge, can be created out of nothing, which means that all ideasâall philosophies, all notions, all future discoveriesâalready exist in people's brains when they are born. Learning is just the process of uncovering that previously imprinted code of laws about the workings of the universe. Since we have a concept of an infinite perfect being in our minds, Descartes then argued that this infinite and perfect beingâGodâmust exist. All other beings are less than divine; they are finite. They all lie somewhere between God and nought. They are a combination of infinity and zero.
However, though zero appeared and reappeared throughout Descartes's philosophy, Descartes insisted unto his death that the voidâthe ultimate zeroâdoes not exist. A child of the Counter-Reformation, Descartes learned about Aristotle at the very moment when the church was relying upon his principles the most. As a result, Descartes, indoctrinated with the Aristotelian philosophy, denied the existence of the vacuum.

Figure 21: A parabola, a circle, and an elliptic curve
It was a difficult position to take; Descartes was certainly mindful of the metaphysical problems of rejecting the vacuum entirely. Later in his life he wrote about atoms and the vacuum: “About these things that involve a contradiction, it can absolutely be said that they cannot happen. However, one shouldn't deny that they can be done by God, namely, if he were to change the laws of nature.” Yet, like the medieval scholars before him, Descartes believed that nothing truly moved in a straight line, for that would leave a vacuum behind it. Instead, everything in the universe moved in a circular path. It was a truly Aristotelian way of thinkingâyet the void would soon unseat Aristotle once and for all.
Even today, children are taught “Nature abhors a vacuum,” while the teachers don't really understand where that phrase came from. It was an extension of the Aristotelian philosophy: vacuums don't exist. If someone would attempt to create a vacuum, nature would do anything in its power to prevent it from happening. It was Galileo's secretary, Evangelista Torricelli, who proved that this wasn't trueâby creating the first vacuum.
In Italy workmen used a kind of pump, which worked more or less like a giant syringe, to raise water out of wells and canals. This pump had a piston that fitted snugly in a tube. The bottom of the tube was placed in the water, so when the piston was raised, the water level followed the plunger upward.
Galileo heard from a worker that these pumps had a problem: they could only lift water about 33 feet. After that, the plunger kept on going upward, yet the water level stayed the same. It was a curious phenomenon, and Galileo passed the problem on to his assistant, Torricelli, who started doing experiments, trying to figure out the reason for the pumps' curious limitation. In 1643, Torricelli took a long tube that was closed at one end and filled it with mercury. He upended it, placing the open end in a dish also filled with mercury. Now, if Torricelli had upended the tube in air, everyone would expect the mercury to run out, because it would quickly be replaced by air; no vacuum would be created. But when it was upended in a dish of mercury, there was no air to replace the mercury in the tube. If nature truly abhorred a vacuum so much, the mercury in the tube would have to stay put so as not to create a void. The mercury didn't stay put. It sank downward a bit, leaving a space at the top. What was in that space? Nothing. It was the first time in history anyone had created a sustained vacuum.
No matter the dimensions of the tube that Torricelli used, the mercury would sink down until its highest point was about 30 inches above the dish; or, looking at it another way, mercury could only rise 30 inches to combat the vacuum above it. Nature only abhorred a vacuum as far as 30 inches. It would take an anti-Descartes to explain why.
In 1623, Descartes was twenty-seven, and Blaise Pascal, who would become Descartes's opponent, was zero years old. Pascal's father, Ãtienne, was an accomplished scientist and mathematician; the young Blaise was a genius equal to his father. As a young man, Blaise invented a mechanical calculating machine, named the Pascaline, which is similar to some of the mechanical calculators that engineers used before the invention of the electronic calculator.