Zero (9 page)
Authors: Charles Seife

The Gaping Void
It was not absolute nothingness. It was a kind of formlessness without any definitionâ¦. True reasoning convinced me that I should wholly subtract all remnants of every kind of form if I wished to conceive the absolutely formless. I could not achieve this.
âS
AINT
A
UGUSTINE
,
C
ONFESSIONS
It's hard to blame the monks for their ignorance. The world of Dionysius Exiguus, Boethius, and Bede was dark indeed. Rome had collapsed, and Western civilization seemed but a shadow of Rome's past glory. The future seemed more horrid than the past. It is no wonder that in the search for wisdom medieval scholars didn't look to their peers for ideas. Instead, they turned to the ancients like Aristotle and the Neoplatonists. As these medieval thinkers imported the philosophy and science of the ancients, they inherited the ancient prejudices: a fear of the infinite and a horror of the void.
Medieval scholars branded void as evilâand evil as void. Satan was quite literally nothing. Boethius made the argument as follows: God is omnipotent. There is nothing God cannot do. But God, the ultimate goodness, cannot do evil. Therefore evil is nothing. It made perfect sense to the medieval mind.
Lurking underneath the veil of medieval philosophy, however, was a conflict. The Aristotelian system was Greek, but the Judeo-Christian story of creation was Semiticâand Semites didn't have such a fear of the void. The very act of creation was out of a chaotic void, and theologians like Saint Augustine, who lived in the fourth century, tried to explain it away by referring to the state before creation as “a nothing something” that is empty of form but yet “falls short of utter nothingness.” The fear of the void was so great that Christian scholars tried to fix the Bible to match Aristotle rather than vice versa.
Luckily, not all civilizations were so afraid of zero.
3
Nothing Ventured
[ ZERO GOES EAST ]
Where there is the Infinite there is joy. There is no joy in the finite.
âT
HE
C
HANDOGYA
U
PANISHAD
T
hough the West was afraid of the void, the East welcomed it. In Europe, zero was an outcast, but in India and later in the Arab lands, it flourished.
When we last saw zero, it was simply a placeholder. It was a blank spot in the Babylonian system of numeration. Zero was useful but was not truly a number on its ownâit had no value. It only took its meaning from the digits to its left; the symbol for zero literally meant nothing if it was by itself. In India, all this changed.
In the fourth century
BC
, Alexander the Great marched with his Persian troops from Babylon to India. It was through this invasion that Indian mathematicians first learned about the Babylonian system of numbersâand about zero. When Alexander died in 323
BC
, his squabbling generals split his empire into pieces. Rome rose to power in the second century
BC
and swallowed up Greece, but Rome's power did not extend as far east as Alexander's had. As a result, remote India was insulated from the rise of Christianity and the fall of Rome in the fourth and fifth centuries
AD
.
India was also insulated from Aristotle's philosophy. Though Alexander had been tutored by Aristotle, and no doubt introduced India to Aristotelian ideas, the Greek philosophy never took hold. Unlike Greece, India never had a fear of the infinite or of the void. Indeed, it embraced them.
The void had an important place in the Hindu religion. Hinduism had started off as a polytheistic religion, a set of tales about warrior gods and battles similar in many ways to the Greek mythos. However, over centuriesâcenturies before Alexander arrivedâthe gods began to merge together. While Hinduism retained its popular rituals and devotion to its pantheon, at its core Hinduism became monotheistic and introspective. All the gods became aspects of an all-encompassing god, Brahma. At about the same time that the Greeks were rising in the Western world, Hinduism was becoming less like the Western myths; the individual gods became less distinct and the religion became more and more mystical. The mysticism was patently Eastern.
Like many Eastern religions, Hinduism was steeped in the symbolism of duality. (Of course, this idea occasionally came up in the Western world, where it was promptly branded as heretical. One example is the Manichaean heresy, which saw the world as being under the influence of equal and opposite sources of good and evil.) As with the yin and yang of the Far East and Zoroaster's dualism of good and evil in the Near East, creation and destruction were intermingled in Hinduism. The god Shiva was both creator and destroyer of the world and was depicted with the drum of creation in one hand and a flame of destruction in another (Figure 13). However, Shiva also represented nothingness. One aspect of the deity, Nishkala Shiva, was literally the Shiva “without parts.” He was the ultimate void, the supreme nothingâlifelessness incarnate. But out of the void, the universe was born, as was the infinite. Unlike the Western universe, the Hindu cosmos was infinite in extent; beyond our own universe were innumerable other universes.

Figure 13: Shiva's dance
At the same time, though, the cosmos never truly abandoned its original emptiness. Nothingness was what the world came from, and to achieve nothingness again became the ultimate goal of mankind. In one story, Death tells a disciple about the soul: “Concealed in the heart of all beings is the Atman, the Spirit, the Self,” he says. “Smaller than the smallest atom, greater than the vast spaces.” This Atman, which resides in every thing, is part of the essence of the universe, and is immortal. When a person dies, the Atman is released from the body and soon enters another being; the soul transmigrates and the person is reincarnated. The goal of the Hindu is to free the Atman entirely from the cycle of rebirth, to stop wandering from death to death. The way to achieve the ultimate liberation through lifelessness is to cease paying heed to the illusion of reality. “The body, the house of the spirit, is under the power of pleasure and pain,” explains a god. “And if a man is ruled by his body then this man can never be free.” But once you are able to separate yourself from the whims of the flesh and embrace the silence and nothingness of your soul, you will be liberated. Your Atman will fly from the web of human desire and join the collective consciousnessâthe infinite soul that suffuses the universe, at once everywhere and nowhere at the same time. It is infinity, and it is nothing.
So India, as a society that actively explored the void and the infinite, accepted zero.
Zero's Reincarnation
In the earliest age of the gods, existence was born from non-existence.
âT
HE
R
IG
V
EDA
Indian mathematicians did more than simply accept zero. They transformed it, changing its role from mere placeholder to number. This reincarnation was what gave zero its power.
The roots of Indian mathematics are hidden by time. An Indian text written the same year that Rome fellâ476
AD
âshows the influence of Greek, Egyptian, and Babylonian mathematics, brought by Alexander as he penetrated Indian lands. Like the Egyptians, the Indians had rope stretchers to survey fields and lay out temples. They also had a sophisticated system of astronomy; like the Greeks, they tried to calculate the distance to the sun. That requires trigonometry; the Indian version was probably derived from the system that the Greeks had developed.
Sometime around the fifth century
AD
, Indian mathematicians changed their style of numbering; they moved from a Greek-like system to a Babylonian-style one. An important difference between the new Indian number system and the Babylonian style was that Indian numbers were base-10 instead of base-60. Our numbers evolved from the symbols that the Indians used; by rights they should be called Indian numerals rather than Arabic ones (Figure 14).
Nobody knows when the Indians made the switch to a Babylonian-style place-value number system. The earliest reference to the Hindu numerals comes from a Syrian bishop who wrote, in 662, of how the Indians did calculations “by means of nine signs.” Nineânot ten. Zero was evidently not among them. But it's hard to tell for sure. It is fairly clear that the Hindu numerals were around before the bishop wrote about them; there is evidence that zero appeared in some variants of the Indian system by that time, though the bishop hadn't heard about it. In any case, a symbol for zeroâthe placeholder in the base-10 numbering systemâwas certainly in use by the ninth century. By then Indian mathematicians had already made a giant leap.
The Indians had borrowed little of Greek geometry. They apparently didn't have a deep interest in the plane figures that the Greeks loved so much. They never worried about whether the diagonal of a square was rational or irrational, nor did they investigate the conic sections as Archimedes had. But they did learn how to play with numbers.
The Indian system of numbering allowed them to use fancy tricks to add, subtract, multiply, and divide numbers without using an abacus to help them. Thanks to their place-number system, they could add and subtract large numbers in roughly the same way we do today. With training, a person could multiply with Indian numerals faster than an abacist could tally. Contests between the abacists and the so-called algorists who used Indian numerals were the medieval equivalents of the Kasparov versus Deep Blue chess match (Figure 15). Like Deep Blue, the algorists would win in the end.
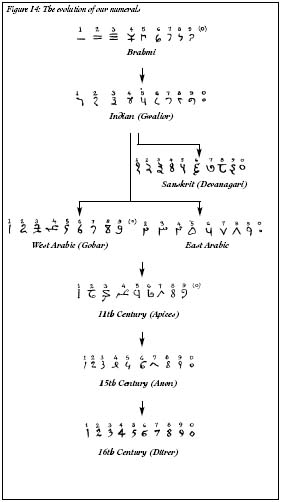
Figure 14: The evolution of our numerals
Though the Indian number system was useful for everyday tasks like addition and multiplication, the true impact of Indian numbers was considerably deeper. Numbers had finally become distinct from geometry; numbers were used to do more than merely measure objects. Unlike the Greeks, the Indians did not see squares in square numbers or the areas of rectangles when they multiplied two different values. Instead, they saw the interplay of numeralsânumbers stripped of their geometric significance. This was the birth of what we now know as
algebra
. Though this mind-set prevented the Indians from contributing much to geometry, it had another, unexpected effect. It freed the Indians from the shortcomings of the Greek system of thoughtâand their rejection of zero.

Figure 15: An algorist versus an abacist
Once numbers shed their geometric significance, mathematicians no longer had to worry about mathematical operations making geometric sense. You can't remove a three-acre swath from a two-acre field, but nothing prevents you from subtracting three from two. Nowadays we recognize that 2 â 3 = â1: negative one. However, this was not at all obvious to the ancients. Many times they solved equations only to get a negative result and concluded that their answer had no meaning. After all, if you are thinking in geometric terms, what is a negative area? It simply didn't make any sense to the Greeks.
To the Indians, negative numbers made perfect sense. Indeed, it was in India (and in China) that negative numbers first appeared. Brahmagupta, an Indian mathematician of the seventh century, gave rules for dividing numbers by each other, and he included the negatives. “Positive divided by positive, or negative by negative, is affirmative,” he wrote. “Positive divided by negative is negative. Negative divided by affirmative is negative.” These are the rules that we recognize today: divide two numbers and the answer is positive if the numbers' signs are the same.
Just as 2 â 3 was now a number, so was 2 â 2. It was zero. Not just a mere placeholder zero that represents an empty space on the abacus, but zero the number. It had a specific value, a fixed place on the number line. Since zero was equal to 2 â 2, then it had to be placed between one (2 â 1) and negative one (2 â 3). Nothing else made sense. No longer could zero sit to the right of nine, just as it does on the top of the computer keyboard; zero had a position in the number line that was all its own. A number line without zero could no more exist than a number system without two. Zero had finally arrived.
However, even the Indians thought that zero was a pretty bizarre number, for all the usual reasons. After all, zero multiplied by anything is zero; it sucks everything into itself. And when you divide with it, all hell breaks loose. Brahmagupta tried to figure out what 0 ÷ 0 and 1 ÷ 0 were, and failed. “Cipher divided by cipher is naught,” he wrote. “Positive or negative divided by cipher is a fraction with that for a denominator.” In other words, he thought 0 ÷ 0 was 0 (he was wrong, as we will see), and he thought that 1 ÷ 0 was, well, we don't really know, because he doesn't make a whole lot of sense. Basically, he was waving his hands and hoping that the problem would go away.