Zero (21 page)
Authors: Charles Seife

If you've got a circle that goes through the north pole of the ball, the shadow is no longer a circle. It is a line. The north pole is like the point at infinity that Kepler and Poncelet imagined. Lines on the plane are simply circles on the sphere that go through the north poleâthe point at infinity (Figure 37).

Figure 36: Stereographic projection of the globe
Once Riemann saw that the complex plane (with a point at infinity) was the same thing as a sphere, mathematicians could see multiplication, division, and other, more difficult operations by analyzing the way the sphere deformed and rotated. For instance, multiplying by the number
i
was equivalent to spinning the sphere 90 degrees clockwise. If you take a number
x
and replace it with (
x
- 1)/(
x
+ 1), that is equivalent to rotating the whole globe by 90 degrees so that the north and south poles lie on the equator (Figures 38, 39, 40). Most interesting of all, if you take a number
x
and replace it with its reciprocal 1/
x,
that is equivalent to flipping the sphere upside down and reflecting it in a mirror. The north pole becomes the south pole and the south pole becomes the north pole: zero becomes infinity and infinity becomes zero. It's all built into the geometry of the sphere; 1/0 =? and 1/?= 0. Infinity and zero are simply opposite poles on the Riemann sphere, and they can switch places in a blink. And they have equal and opposite powers.
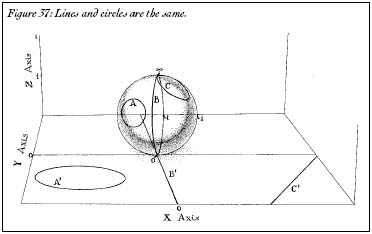
Figure 37: Lines and circles are the same.
Take all of the numbers in the complex plane and multiply them by two. That is like putting your hands on the south pole and stretching a rubber cover on the sphere away from the south pole and toward the north pole. Multiplying by one-half has the opposite effect. It is like stretching the rubber cover away from the north pole and toward the south pole. Multiplying by infinity is like sticking a needle in the south pole; the rubber sheet all flings upward toward the north pole: anything times infinity is infinity. Multiplying by zero is like sticking a needle on the north pole and everything winds up at zero: anything times zero is zero. Infinity and zero are equal and oppositeâand equally destructive.
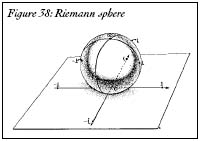
Figure 38: Riemann sphere
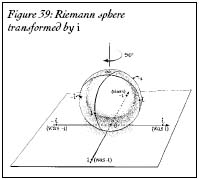
Figure 39: Riemann sphere transformed by i
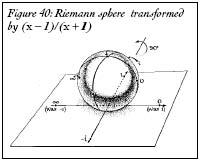
Figure 40: Riemann sphere transformed by
(x - 1)/(x + 1)
Zero and infinity are eternally locked in a struggle to engulf all the numbers. Like a Manichaean nightmare, the two sit on opposite poles of the number sphere, sucking numbers in like tiny black holes. Take any number on the plane. For the sake of argument, we'll choose
i
/2. Square it. Cube it. Raise it to the fourth power. The fifth. The sixth. The seventh. Keep multiplying. It slowly spirals toward zero like water down a drain. What happens to 2
i
? The exact opposite. Square it. Cube it. Raise it to the fourth power. It spirals outward (Figure 41). But on the number sphere, the two curves are duplicates of each other; they are mirror images (Figure 42). All numbers in the complex plane suffer this fate. They are drawn inexorably toward 0 or toward ?. The only numbers that escape are the ones that are equally distant from the two rivalsâthe numbers on the equator, like 1, -1, and
i.
These numbers, pulled by the tug of both zero and infinity, spiral around on the equator forever and ever, never able to escape the grasp of either. (You can see this on your calculator. Enter a numberâany number. Square it. Square it again. Do it again and again; the number will quickly zoom toward infinity or toward zero, except if you entered 1 or -1 to begin with. There is no escape.)
The Infinite Zero
My theory stands as firm as a rock; every arrow directed against it will return quickly to its archer. How do I know this? I have studied itâ¦I have followed its roots, so to speak, to the first infallible cause of all created things.
âG
EORG
C
ANTOR
Infinity was no longer mystical; it became an ordinary number. It was a specimen impaled on a pin, ready for study, and mathematicians were quick to analyze it. But in the deepest infinityânestled within the vast continuum of numbersâzero kept appearing. Most appalling of all, infinity itself can be a zero.
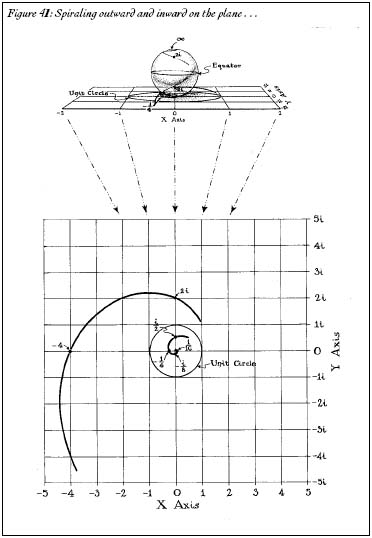
Figure 41: Spiraling outward and inward on the planeâ¦
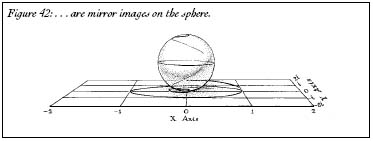
Figure 42:â¦are mirror images on the sphere.
In the old days, before Riemann saw that the complex plane was really a sphere, functions like 1/
x
would stump mathematicians. When
x
goes to zero, 1/
x
gets bigger and bigger and bigger and finally just blows up and goes off to infinity. Riemann made it perfectly acceptable to go off to infinity; since infinity is just a point on the sphere like any other point, it was no longer something to be feared. In fact, mathematicians started analyzing and classifying the points where a function blows up:
singularities.
The curve 1/
x
has a singularity at the point
x
= 0âa very simple sort of singularity that mathematicians dubbed a
pole.
There are other types of singularities as well; for instance, the curve sin(1/
x
) has an
essential
singularity at
x
= 0. Essential singularities are weird beasts; near a singularity of this sort, a curve goes absolutely berserk. It oscillates up and down faster and faster as it approaches the singularity, whipping from positive to negative and back again. In even the tiniest neighborhood around the singularity, the curve takes on almost every conceivable value over and over and over again. Yet as weird as these singularities behave, they were no longer mysterious to mathematicians, who were learning to dissect the infinite.
The master anatomist of the infinite was Georg Cantor. Though he was born in Russia in 1845, Cantor spent most of his life in Germany. And it was in Germanyâthe land of Gauss and of Riemannâwhere infinity's secrets were revealed. Unfortunately, Germany was also the land of Leopold Kronecker, the mathematician who would hound Cantor into a mental institution.
Underneath Cantor's conflict with Kronecker was a vision of the infinite, a vision that can be described with a simple puzzle. Imagine that there is a large stadium filled with people and you want to know whether there are more seats, more people, or an equal number of both. You could count the number of people and count the number of seats and then compare the two numbers, but that would take a lot of time. There's a much cleverer way. Just ask everyone to sit down in a seat. If there are empty seats, then there are too few people. If people remain standing, there are too few seats. If every seat is filled and nobody is left standing, then the number of people and seats are equal.