Zero (24 page)
Authors: Charles Seife

Rayleigh and Jeans had done nothing wrong. They used equations that physicists thought were valid, manipulated them in an accepted way, and came out with an answer that didn't reflect the way the world works. Ice cubes don't wipe out civilizations with bursts of gamma rays, though following the then-accepted rules of physics led inexorably to that conclusion. One of the laws of physics had to be wrong. But which one?
The Quantum Zero: Infinite Energy
To physicists, vacuum has all particles and forces latent in it. It's a far richer substance than the philosopher's nothing.
âS
IR
M
ARTIN
R
EES
The ultraviolet catastrophe led to the quantum revolution. Quantum mechanics got rid of the zero in the classical theory of lightâremoving the infinite energy that supposedly came from every bit of matter in the universe. However, this was not much of a victory. A zero in quantum mechanics means that the entire universeâincluding the vacuumâis filled with an infinite amount of energy: the
zero-point
energy. This, in turn, leads to the most bizarre zero in the universe: the phantom force of nothing.
In 1900, German experimenters tried to shed some light on the ultraviolet catastrophe. By making careful measurements of how much radiation came off objects at various temperatures, they showed that the Rayleigh-Jeans formula was, indeed, failing to predict the true amount of light that comes from objects. A young physicist named Max Planck looked at the new data and within hours came up with a new equation that replaced the Rayleigh-Jeans formula. Not only did Planck's formula explain the new measurements, it solved the ultraviolet catastrophe. The Planck formula did not zoom off to infinity as the wavelength decreased; instead of having the energy get bigger and bigger as the wavelength goes down, it got smaller and smaller again (Figure 47). Unfortunately, though Planck's formula was correct, its repercussions were more troubling than the ultraviolet catastrophe it solved.
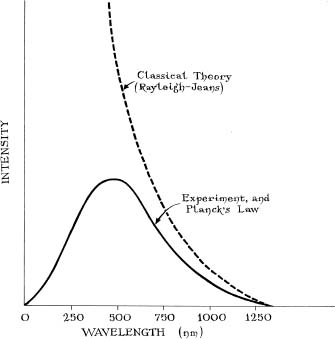
Figure 47: Rayleigh-Jeans goes off to infinity, but Planck stays finite.
The problem arose because the ordinary assumptions of statistical mechanicsâthe laws of physicsâdid not lead Planck to his formula. The laws of physics had to change to accommodate the Planck formula. Planck later described what he did as an “act of desperation”; nothing less than desperation would compel a physicist to make such a seemingly nonsensical change in the laws of physics: According to Planck, molecules are forbidden to move in most ways. They vibrate only with certain acceptable energies, called quanta. It is impossible for molecules to have energies in between these acceptable values.
This might not seem like such a strange assumption, but it is not the way the world seems to work. Nature doesn't move in jumps. It would seem silly to have five-foot-tall people and six-foot-tall people but nothing in between. It would be ridiculous if cars drove at 30 miles an hour and 40 miles an hour, but never at 33 or 38 miles an hour. However, a quantum car would behave in exactly this way. You might be driving along at 30 miles an hour, but when you step on the gas, all of a sudden you would instantlyâpop!âbe driving 40 miles an hour. Nothing in between is allowed, so to get from 30 to 40 miles an hour, you have to make a
quantum leap.
In the same way, quantum people could not grow very easily; they would hover at four feet for a number of years, and then, in a fraction of a secondâpop!âthey would be five feet tall. The quantum hypothesis violates everything our everyday experience tells us.
Even though it doesn't agree with the way nature seems to work, Planck's strange hypothesisâthat molecular vibrations were
quantized
âled to the correct formula for the frequencies of light that come off an object. Even though physicists quickly realized that Planck's equation was right, they did not accept the quantum hypothesis. It was too bizarre to accept.
An unlikely candidate would turn the quantum hypothesis from a pecularity to an accepted fact. Albert Einstein, a twenty-six-year-old patent clerk, showed the physics world that nature worked in quanta rather than in smooth increments. He would later become the chief opponent of the theory he helped create.
Einstein didn't seem like a revolutionary. When Max Planck was turning the physics world on its head, Albert Einstein was scrambling for a job. Out of money, he took a temporary position at the Swiss patent office, a far cry from the assistantship at a university that he wanted. By 1904 he was married, had a newborn son, and was laboring in the patent officeâhardly the path to greatness. However, in March 1905, he wrote a paper that would eventually earn him the Nobel Prize. This paperâwhich explained the
photoelectric effect,
brought quantum mechanics into the mainstream. Once quantum mechanics was accepted, so, too, would the mysterious powers of zero.
The photoelectric effect was discovered in 1887 when the German physicist Heinrich Hertz discovered that a beam of ultraviolet light could cause a plate to spark: electrons quite simply pop out of the metal when light shines on it. This phenomenon, causing sparks with a beam of light, was very puzzling to classical physicists. Ultraviolet light is light with a lot of energy, so scientists naturally concluded that it took quite a bit of energy to kick an electron out of an atom. But according to the wave theory of light, there is another way to get high-energy light: make it brighter. A very bright blue light, for instance, might have as much energy as a dim ultra-violet beam; therefore, a bright blue light should be able to kick electrons out of atoms, just as a dim ultraviolet beam can.
This simply is not the case, as experiments quickly showed. Even a dim beam of ultraviolet (high frequency) light causes electrons to get knocked out of the metal. However, if you lower the frequency just a little bit beyond a critical thresholdâmaking the light a wee bit too redâthe sparking stops all of a sudden. No matter how bright the beam is, if the light is the wrong color, all the electrons in the metal stay put; none of them can escape. That's not the sort of thing a light wave would do.
Einstein solved this quandaryâthe puzzle of the photo-electric effectâbut his solution was even more revolutionary than Planck's hypothesis. While Planck proposed that molecules' vibrations were quantized, Einstein proposed that light came in little packets of energy called photons. This idea conflicted with the accepted physics of light, because it meant that light was not a wave.
On the other hand, if light energy is bundled into little packets, then the photoelectric effect is easy to explain. The light is acting like little bullets that get shot into the metal. When a bullet hits an electron, it gives it a nudge. If the bullet has enough energyâif its frequency is high enoughâthen it knocks the electron free. On the other hand, if a light particle doesn't have enough energy to nudge the electron out, then the electron stays put; the photon skitters away instead.
Einstein's idea explained the photoelectric effect brilliantly. Light is quantized into photons, directly contradicting the wave theory of light that had not been questioned for more than a century. Indeed, it turns out that light has
both
a wave nature and a particle nature. Though light acts like a particle sometimes, it acts like a wave at other times. In truth, light is neither particle nor wave, but a strange combination of the two. It's a hard concept to grasp. However, this idea is at the heart of the quantum theory.
According to quantum theory, everythingâlight, electrons, protons, small dogsâhave both wavelike and particle-like properties. But if objects are particles and waves at the same time, what on earth could they be? Mathematicians know how to describe them: they are
wave functions,
solutions to a differential equation called the Schrödinger equation. Unfortunately, this mathematical description has no intuitive meaning; it is all but impossible to visualize what these wave functions are.
*
Worse yet, as physicists discovered the intricacies of quantum mechanics, stranger and stranger things began to appear. Perhaps the weirdest of all is caused by a zero in the equations of quantum mechanics: the zero-point energy.
This strange force is woven into the mathematical equations of the quantum universe. In the mid-1920s a German physicist, Werner Heisenberg, saw that these equations had a shocking consequence: uncertainty. The force of nothing is caused by the Heisenberg uncertainty principle.
The concept of uncertainty pertains to scientists' ability to describe the properties of a particle. For instance, if we want to find a particular particle, we need to determine the particle's position and velocityâwhere it is and how fast it is going. Heisenberg's uncertainty principle tells us that we can't do even this simple act. No matter how hard we try, we cannot measure a particle's position and its velocity with perfect accuracy at the same time. This is because the very act of measuring destroys some of the information we are trying to gather.
To measure something, you need to prod it. For instance, imagine that you are measuring the length of a pencil. You could run your fingers along it and measure how long it is; however, you'll probably give the pencil a nudge, disturbing the pencil's velocity slightly. A better way would be to place a ruler gently next to the pencil, but in fact, comparing the lengths of the two objects also changes the pencil's speed a tiny bit. You can only look at the pencil when light is bouncing off it; though the disturbance is very slight, the photons that carom off the pencil nudge it ever so gently, changing the pencil's velocity a tiny bit. No matter what way you think of to measure the pencil, you will give it a tiny nudge in the process. Heisenberg's uncertainty principle shows that there is no possible way to measure the pencil's lengthâor an electron's positionâand its velocity with perfect accuracy at the same time. In fact, the better you know a particle's position, the less you know about its velocity, and vice versa. If you measure an electron's position with zero errorâyou know exactly where it is at a given momentâyou must have zero information about how fast it is going. And if you know a particle's velocity with infinite precisionâzero errorâyou have infinite error when you measure its position; you know nothing at all about where it is.
*
You can never know both at the same time, and if you have some information about one, you must have some uncertainty about the other. It's another unbreakable law.
Heisenberg's uncertainty principle applies to more than just measurements performed by humans. Like the laws of thermodynamics, the principle applies to nature itself. Uncertainty makes the universe seethe with infinite energy. Imagine an extremely tiny volume in space, like a really small box. If we analyze what is going on inside that box, we can make some assumptions. For instance, we know, with some precision, the position of the particles inside. After all, they can't be outside the box; we know that they are restricted to a certain volume, because if they were outside the box, we would not be looking at them. Because we have some information about the particles' position, the Heisenberg uncertainty principle implies that we must have some uncertainty about the particles' velocityâtheir energy. As we make that box smaller and smaller, we know less and less about the particles' energy.
This argument holds everywhere in the universeâin the center of the earth and in the deepest vacuum of space. This means that in a sufficiently small volume, even in a vacuum, we have some uncertainty about the amount of energy inside. But uncertainty about the energy in a vacuum sounds ridiculous. The vacuum, by definition, has nothing in itâno particles, no light, nothing. Thus, the vacuum should have no energy at all. Yet according to Heisenberg's principle, we cannot know how much energy there is in a volume of the vacuum at any given time. The energy in a tiny volume of vacuum must be fluctuating constantly.
How could the vacuum, which has nothing in it, have any energy at all? The answer comes from another equation: Einstein's famous
E
=
mc
2
. This simple formula relates mass and energy: the mass of an object is equivalent to a certain amount of energy. (In fact, particle physicists don't measure the mass of the electron, say, in kilograms or pounds or any of the usual units of mass or weight. They say that the electron's
rest mass
is 0.511 MeV [million electron volts]âa lump of energy.) The fluctuation in the energy in the vacuum is the same thing as a fluctuation in the amount of mass. Particles are constantly winking in and out of existence, like tiny Cheshire cats. The vacuum is never truly empty. Instead, it is seething with these
virtual particles;
at every point in space, an infinite number are happily popping up and disappearing. This is the zero-point energy, an infinity in the formulas of quantum theory. Interpreted strictly, the zero-point energy is limitless. According to the equations of quantum mechanics, more power than is stored in all the coal mines, oil fields, and nuclear weapons in the world is sitting in the space inside your toaster.