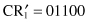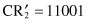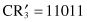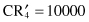Data Mining (114 page)
Authors: Mehmed Kantardzic

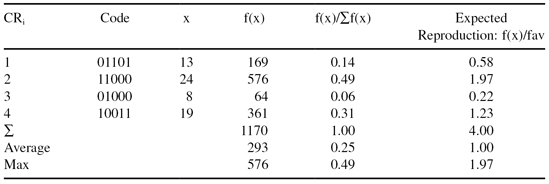
TABLE 13.2.
Evaluation of the Initial Population
13.3.4 Alternation
In the alternation phase, the new population is selected based on the population evaluated in the previous iteration. Clearly, the chromosome CR
4
in our example is the best of the four chromosomes, since its evaluation returns the highest value. In the alternation phase, an individual may be selected depending on its objective-function value or fitness value. For maximization problems, the higher the individual’s fitness is, the more probable that it can be selected for the next generation. There are different schemes that can be used in the selection process. In the simple GA we proposed earlier, the roulette wheel selection technique, an individual is selected randomly depending on a computed probability of selection for each individual. The probability of selection is computed by dividing the individual’s fitness value by the sum of fitness values of the corresponding population, and these values are represented in column 5 of Table
13.2
.
In the next step we design the roulette wheel, which is, for our problem, graphically represented in Figure
13.4
.
Figure 13.4.
Roulette wheel for selection of the next population.
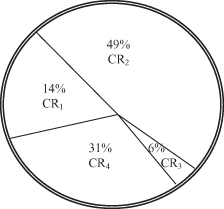
Using the roulette wheel, we can select chromosomes for the next population. Suppose that the randomly selected chromosomes for the next generation are CR
1
, CR
2
, CR
2
, CR
4
(the selection is in accordance with the expected reproduction—column 6 in Table
13.2
). In the next step, these four chromosomes undergo the genetic operations: crossover and mutation.
13.3.5 Genetic Operators
Crossover is not necessarily applied to all pairs of selected individuals. A choice is made depending on a specified probability called PC, which is typically between 0.5 and 1. If crossover is not applied (PC = 0), the offspring are simply a duplication of the parents. For the process of crossover it is necessary to determine the percentage of the population that will perform the crossover. For our particular problem we use the following parameters of the GA:
1.
population size,
pop-size
= 4 (the parameter was already used).
2.
probability of crossover, PC = 1.
3.
probability of mutation, PM = 0.001 (the parameter will be used in a mutation operation).
A value of 1 for the probability of crossover translates into a 100% crossover—all chromosomes will be included in the crossover operation.
The second set of parameters in this phase of a GA is the random selection of parents for crossover and positions in the strings where the crossover will be performed. Suppose that these are randomly selected pairs: CR
1
–CR
2
and CR
2
–CR
4
, and crossover is after the third position in the strings for both pairs. Then the selected strings
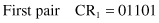
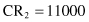
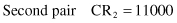
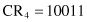
will become, after crossover, a new population: