Data Mining (64 page)
Authors: Mehmed Kantardzic

Figure 7.11.
Generalization as a problem of curve fitting. (a) A fitting curve with good generalization; (b) overfitted curve.
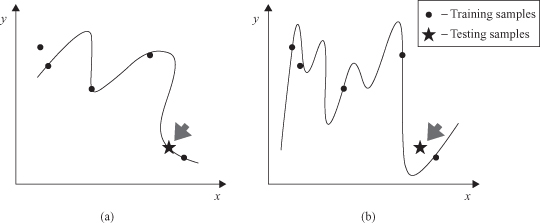
To overcome the problem of overfitting, some additional practical recommendations may be introduced for the design and application of ANN in general and multiplayer perceptrons in particular. In ANNs, as in all modeling problems, we want to use the simplest network that can adequately represent the training data set. Do not use a bigger network when a smaller network will work. An alternative to using the simplest network is to stop the training before the network overfits. Also, one very important constraint is that the number of network parameters should be limited. For a network to be able to generalize it should have fewer parameters (significantly) than there are data points in the training set. ANN generalization is extremely poor if there is a large input space with very few training samples.
Interpretability of data-mining models including ANNs, or the understanding of the way inputs relate to an output in a model, is a desirable property in applied data-mining research because the intent of such studies is to gain knowledge about the underlying reasoning mechanisms. Interpretation may also be used to validate results that are inconsistent or contradictory to common understanding of issues involved, and it may also indicate problems with data or models.
While ANNs have been intensively studied and successfully used in classification and regression problems, their interpretability still remains vague. They suffer from the shortcoming of being “black boxes,” that is, without explicit mechanisms for determining why an ANN makes a particular decision. That is, one provides the input values for an ANN and obtains an output value, but generally no information is provided regarding how those outputs were obtained, how the input values correlate to the output value, and what is the meaning of large numbers of weight factors in the network. ANNs acceptability as valid data-mining methods for business and research requires that beyond providing excellent predictions they provide meaningful insight that can be understood by a variety of users: clinicians, policy makers, business planners, academicians, and lay persons. Human understanding and acceptance is greatly enhanced if the input–output relations are explicit, and end users would gain more confidence in the prediction produced.
Interpretation of trained ANNs can be considered in two forms: broad and detailed. The aim of a broad interpretation is to characterize how important an input neuron is for predictive ability of the model. This type of interpretation allows us to rank input features in order of importance. The broad interpretation is essentially a sensitivity analysis of the neural network. The methodology does not indicate the sign or direction of the effect of each input. Thus, we cannot draw conclusions regarding the nature of the correlation between input descriptors and network output; we are only concluding about the level of influence.
The goal of a detailed interpretation of an ANN is to extract the structure-property trends from an ANN model. For example, each of the hidden neurons corresponds to the number of piecewise hyperplanes that are components available for approximating the target function. These hyperplanes act as the basic building blocks for constructing an explicit ANN model. To obtain a more comprehensible system that approximates the behavior of the ANN, we require the model with less complexity, and at the same time maybe scarifying accuracy of results. The knowledge hidden in a complex structure of an ANN may be uncovered using a variety of methodologies that allow mapping an ANN into a rule-based system. Many authors have focused their activities on compiling the knowledge captured in the topology and weight matrix of a neural network into a symbolic form: some of them into sets of ordinary if-then rules, others into formulas from propositional logic or from non-monotonic logics, or most often into sets of fuzzy rules. These transformations make explicit the knowledge implicitly captured by the trained neural network and it allows the human specialist to understand how the neural network generates a particular result. It is important to emphasize that any method of rule extraction from ANN is valuable only to the degree to which the extracted rules are meaningful and comprehensible to a human expert.
It is proven that the best interpretation of trained ANNs with continuous activation functions is in a form of fuzzy rule-based systems. In this way, a more comprehensible description of the action of the ANN is achieved. Multilayer feedforward ANNs are seen as additive fuzzy rule-based systems. In these systems, the outputs of each rule are weighted by the activation degree of the rule, and then they are added for an integrated representation of an ANN model. The main disadvantage of most approximation techniques of neural networks by fuzzy rules is the exponential increase of required number of rules for a good approximation. Fuzzy rules that express the input–output mapping of the ANNs are extracted using different approaches described in numerous references. If the reader is interested for more details about methodologies, the starting points may be the recommended references at the end of this chapter, and also the introductory concepts about fuzzy systems given in Chapter 14.
7.6 COMPETITIVE NETWORKS AND COMPETITIVE LEARNING
Competitive neural networks belong to a class of recurrent networks, and they are based on algorithms of unsupervised learning, such as the competitive algorithm explained in this section. In competitive learning, the output neurons of a neural network compete among themselves to become active (to be “fired”). Whereas in multiplayer perceptrons several output neurons may be active simultaneously, in competitive learning only a single output neuron is active at any one time. There are three basic elements necessary to build a network with a competitive learning rule, a standard technique for this type of ANNs:
1.
a
set of neurons
that have the same structure and that are connected with initially randomly selected weights; therefore, the neurons respond differently to a given set of input samples;
2.
a
limit value
that is determined on the strength of each neuron; and
3.
a
mechanism that permits the neurons to compete
for the right to respond to a given subset of inputs, such that only one output neuron is active at a time. The neuron that wins the competition is called winner-take-all neuron.
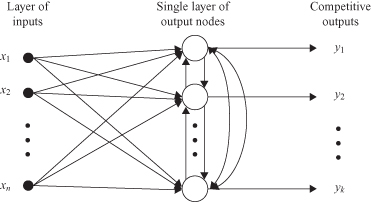
In the simplest form of competitive learning, an ANN has a single layer of output neurons, each of which is fully connected to the input nodes. The network may include feedback connections among the neurons, as indicated in Figure
7.12
. In the network architecture described herein, the feedback connections perform
lateral inhibition
, with each neuron tending to inhibit the neuron to which it is laterally connected. In contrast, the feedforward synaptic connections in the network of Figure
7.12
are all
excitatory
.
Figure 7.12.
A graph of a simple competitive network architecture.
For a neuron k to be the winning neuron, its net value net
k
for a specified input sample X = {x
1
, x
2
, … , x
n
} must be the largest among all the neurons in the network. The output signal y
k
of the winning neuron k is set equal to one; the outputs of all other neurons that lose the competition are set equal to 0. We thus write
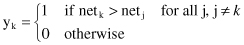
where the induced local value net
k
represents the combined action of all the forward and feedback inputs to neuron k.
Let w
kj
denote the synaptic weights connecting input node j to neuron k. A neuron then learns by shifting synaptic weights from its inactive input nodes to its active input nodes. If a particular neuron wins the competition, each input node of that neuron relinquishes some proportion of its synaptic weight, and the weight relinquished is then distributed among the active input nodes. According to the standard, competitive-learning rule, the change Δw
kj
applied to synaptic weight w
kj
is defined by

where η is the learning-rate parameter. The rule has the overall effect of moving the synaptic weights of the winning neuron toward the input pattern X. We may use the geometric analogy represented in Figure
7.13
to illustrate the essence of competitive learning.
Figure 7.13.
Geometric interpretation of competitive learning. (a) Initial state of the network; (b) final state of the network.
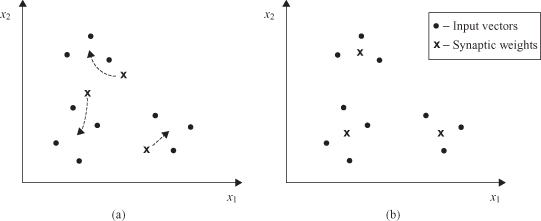
Each output neuron discovers a cluster of input samples by moving its synaptic weights to the center of gravity of the discovered cluster. Figure
7.13
illustrates the ability of a neural network to perform clustering through competitive learning. During the competitive-learning process, similar samples are grouped by the network and represented by a single artificial neuron at the output. This grouping, based on data correlation, is done automatically. For this function to be performed in a stable way, however, the input samples must fall into sufficiently distinct groups. Otherwise, the network may be unstable.