Financial Markets Operations Management (12 page)
Read Financial Markets Operations Management Online
Authors: Keith Dickinson

ETD products are predominantly futures and options contracts that have been created by derivatives exchanges and centrally cleared through a clearing house. These products are standardised in terms of underlying assets, exercise dates and trading â all elements of the product's contract specification.
These contracts are created as required by the users; there are no limits regarding total contracts. However, to gain an idea of the depth of the market, users need to know trading volumes and open interest. This information, together with opening, closing, highest and lowest prices, is published by the derivatives exchange that created the product.
For the final part of this chapter, we turn our attention to the second type of derivative â over-the-counter, or OTC, derivatives.
Unlike exchange-traded derivatives, OTC derivatives are not created by an exchange with standardised contract specifications, trading rules, etc. Instead, OTC derivatives are privately negotiated between buyer and seller away from any exchange. This results in issues that have concerned the industry's regulators:
- As the contracts are not cleared centrally, there is no central counterparty.
- Each counterparty to a trade relies on the other party to perform, and as some OTC contracts can last for many years before termination, there is a high degree of counterparty risk involved.
- As the contracts are not traded on an exchange, there has been no requirement to report trades.
- OTC derivatives can be relatively straightforward in design and content; however, many are highly complex in structure with risks that are correspondingly complex.
- The specification of OTC derivatives is established at the time of the trade. Nevertheless, the more “vanilla” contracts do follow basic templates.
This situation is changing. Due to pressure from the regulators, OTC contracts are migrating to central clearing systems, trades are expected to be reported (whether centrally cleared or not) and there is the possibility that trading itself might migrate to exchanges.
The big question concerns the more complex derivative structures (the exotic derivatives). As there is no central, exchange-published pricing, OTC derivatives can be very difficult to value. If the clearing houses do not understand the risks of the products and find it difficult to value them, they might decide not to clear them. Consequently, the usage of exotic derivatives could decrease or disappear altogether.
When we trade forward and swap products, we talk about a
notional amount
. With the exception of currency swaps, the notional amount is never exchanged â only the payments generated by the notional amount are exchanged.
A good source of information regarding notional amounts outstanding and gross market values of OTC derivatives can be found in the statistical annex of the Bank for International Settlements' “Quarterly Review”.
11
In the BIS Quarterly Review for December 2013, Table 19, “Amounts outstanding of over-the-counter (OTC) derivatives”, showed the amounts and values for the main risk categories given in
Table 2.49
.
TABLE 2.49
BIS â Amounts outstanding of OTC derivatives
| Notional amounts outstanding | Gross market values | |||||||||
| Risk Category / | Â Jun | Dec | Jun | Dec | Jun | Â Jun | Dec | Jun | Dec | Jun |
| Instrument | Â 2011 | 2011 | 2012 | 2012 | 2013 | Â 2011 | 2011 | 2012 | 2012 | 2013 |
| Total contracts | 706,884 | 647,811 | 639,396 | 632,579 | 692,908 | 19,518 | 27,307 | 25,417 | 24,740 | 20,158 |
| Foreign exchange contracts | 64,698 | 63,381 | 66,672 | 67,358 | 73,121 | 2,336 | 2,582 | 2,240 | 2,304 | 2,424 |
| Â Â Â Forwards and forex swaps | 31,113 | 30,526 | 31,395 | 31,718 | 34,421 | 777 | 919 | 771 | 803 | 953 |
| Â Â Â Currency swaps | 22,228 | 22,791 | 24,156 | 25,420 | 24,654 | 1,227 | 1,318 | 1,184 | 1,247 | 1,131 |
| Â Â Â Options | 11,358 | 10,065 | 11,122 | 10,220 | 14,046 | 332 | 345 | 285 | 254 | 339 |
| Interest rate contracts | 553,240 | 504,117 | 494,427 | 489,703 | 561,299 | 13,244 | 20,001 | 19,113 | 18,833 | 15,155 |
| Â Â Â Forward rate agreements | 55,747 | 50,596 | 64,711 | 71,353 | 86,334 | 59 | 67 | 51 | 47 | 168 |
| Â Â Â Interest rate swaps | 441,201 | 402,611 | 379,401 | 369,999 | 425,569 | 11,861 | 18,046 | 17,214 | 17,080 | 13,663 |
| Â Â Â Options | 56,291 | 50,911 | 50,314 | 48,351 | 49,396 | 1,324 | 1,888 | 1,848 | 1,706 | 1,325 |
| Equity-linked contracts | 6,841 | 5,982 | 6,313 | 6,251 | 6,821 | 708 | 679 | 645 | 605 | 693 |
| Â Â Â Forwards and swaps | 2,029 | 1,738 | 1,880 | 2,045 | 2,321 | 176 | 156 | 147 | 157 | 206 |
| Â Â Â Options | 4,813 | 4,244 | 4,434 | 4,207 | 4,501 | 532 | 523 | 497 | 448 | 487 |
| Commodity contracts | 3,197 | 3,091 | 2,994 | 2,587 | 2,458 | 471 | 481 | 390 | 358 | 386 |
| Â Â Â Gold | 468 | 521 | 523 | 486 | 461 | 50 | 75 | 61 | 53 | 30 |
| Â Â Â Other commodities | 2,729 | 2,570 | 2,471 | 2,101 | 1,997 | 421 | 405 | 328 | 306 | 306 |
| Â Â Â Â Â Â Forwards and swaps | 1,846 | 1,745 | 1,659 | 1,363 | 1,327 | |||||
| Â Â Â Â Â Â Options | 883 | 824 | 812 | 739 | 670 | |||||
| Credit default swaps | 32,409 | 28,626 | 26,931 | 25,069 | 24,349 | 1,345 | 1,586 | 1,187 | 848 | 725 |
| Â Â Â Single-name instruments | 18,105 | 16,865 | 15,566 | 14,309 | 13,135 | 854 | 958 | 715 | 527 | 430 |
| Â Â Â Multi-name instruments | 14,305 | 11,761 | 11,364 | 10,760 | 11,214 | 490 | 628 | 472 | 321 | 295 |
| Â Â Â Â Â Â of which index products | 12,473 | 10,514 | 9,731 | 9,663 | 10,170 | |||||
| Unallocated | 46,498 | 42,613 | 42,059 | 41,611 | 24,860 | 1,414 | 1,978 | 1,842 | 1,792 | 775 |
| Memorandum Item: | ||||||||||
| Â Â Â Gross Credit Exposure | 2,971 | 3,939 | 3,691 | 3,609 | 3,900 |
Source:
BIS Quarterly Review March 2014 (online). Available from
www.bis.org/publ/qtrpdf/r_qt1403.htm
. [Accessed Monday, 5 May 2014]
Interest rate contracts have by far the greatest number of notional amounts outstanding and gross market values, at USD 561,299 billion and USD 15,155 billion respectively.
We will look at two examples of a forward contract:
- A forward rate agreement (FRA);
- A currency forward.
An FRA is an obligation to settle the difference between two interest rates calculated on a notional amount. FRAs are used by banks and corporates to hedge interest rate exposures. For example, you are the Treasurer of a corporate that wishes to borrow USD 10,000,000 for six months. If you wanted to borrow today, you would expect to pay the six-month spot rate. Suppose, though, you needed to borrow in three months' time (and not today); what is your risk? Answer: interest rates might rise over the next three months, making the cost of borrowing more expensive.
In order to buy protection against a rate rise, you buy an FRA at a price of 2.00% p.a. (the
fixed rate
) on the notional amount of USD 10,000,000. The price reflects the interest rate on a loan that starts in three months' time and has a term of six months â a 3x9 FRA (nine months less three months = six months).
In three months' time, you observe the spot six-month interest rate to be 2.50% p.a. (the
reference rate
). The rate has increased, as you had previously feared.
The difference in price is 0.50% p.a. (2.50% â 2.00%) and therefore, under the terms of the FRA, the seller pays this difference on the notional amount to the buyer. Once this amount has been paid, the FRA is finished with no further payments to make.
Intuitively, the seller would pay:
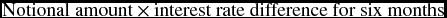
However, the amount payable is paid at the
start
of the six-month loan period and not at the
end
as would normally be the case in lending. In order to make an adjustment to correct this anomaly, the amount payable is discounted by the reference rate. In our example, the amount payable by the seller to you would therefore be USD 24,962.28:

This is assuming 182 actual days in the six-month period.
There are two observations to make:
- If you had wanted to borrow USD 10Â million, you would borrow at the spot rate of 2.50% and receive the FRA difference. This would bring your cost down to almost 2.00%, i.e. the original fixed rate.
- If you simply wanted to speculate on the direction interest rates would go, you would receive the USD 24,962.28 as your winnings on the bet.
Although the payment is not settled until the start of the loan period (the
effective date
), both parties have an interest risk from the moment they enter into the transaction up to the effective date. To cover this risk, the FRA is revalued daily and the party at risk receives collateral. We will cover the topic of collateral later in the book.
In the above example, we used the notation 3Ã9 to denote the effective date and the termination date. See
Table 2.50
for further examples of this notation using LIBOR as the benchmark rate (we could equally have used another interbank rate depending on the circumstances).
TABLE 2.50
FRA notation using LIBOR
| EffectiveDate | TerminationDate | InterestRate | Notation |
| Â 1 month | Â 4 months | 3-LIBOR | 1 Ã 4 |
| Â 1 month | Â 7 months | 6-LIBOR | 1 Ã 7 |
| Â 3 months | Â 6 months | 3-LIBOR | 3 Ã 6 |
| Â 3 months | Â 9 months | 6-LIBOR | 3 Ã 9 |
| Â 6 months | 12 months | 6-LIBOR | 6 Ã 12 |
| 12 months | 18 months | 6-LIBOR | 12 Ã 18 |
In summary, by entering into an FRA, you can lock in an interest rate to protect against an interest rate increase (as in our example). To do this, you would buy an FRA. Conversely, you can lock in an interest rate to protect against an interest rate decrease by selling an FRA.