Más rápido que la velocidad de la luz (14 page)

No obstante, la ley de Hubble tiene una interpretación en la concepción de Friedmann. Según el físico ruso, vivimos en un universo en expansión cuyo modelo sería un espacio en el cual las distancias se multiplican por un número que se denomina
factor de expansión
o
factor de escala.
Este factor aumenta con el transcurso del tiempo, lo que implica una expansión geométrica. Sin embargo, como todas las distancias se multiplican por ese factor, cuanto mayor es la distancia, tanto más grande es el incremento. No ocurriría lo mismo si se sumara un número a todas las distancias, pero ocurre que el factor de expansión es
multiplicativo
: a mayor distancia, mayor es el incremento a lo largo del tiempo.

En consecuencia, si volvemos a la concepción de Hubble y describimos la expansión como un movimiento real en un espacio newtoniano, parece que la "velocidad" es proporcional a la distancia, que es precisamente lo que dice la ley de Hubble. Pero la concepción de Friedmann es más compleja aún, pues muestra que el movimiento hacia afuera que Hubble observó más tarde no tiene realmente un centro: cualquier observador tiene la ilusión de que es el centro de un movimiento hacia afuera —hecho que satisface la ley de Hubble— porque en realidad la totalidad del espacio se estira con igual ritmo en todas partes.

Una vez aclarado este punto, Friedmann postuló, como Einstein, que el fluido cosmológico es homogéneo, es decir, tiene el mismo aspecto o las mismas propiedades en todo el universo. Más que provenir de los datos, los motivos para formular ese postulado son intuitivos y de conveniencia matemática (por no hablar de haraganería). Debemos recordar que todos esos razonamientos se hicieron años antes del descubrimiento de Hubble. De hecho, por respeto al rigor histórico, tanto Einstein como Friedmann pensaron en un fluido homogéneo de estrellas, y no de galaxias, de las cuales no tenían noticia. Por un verdadero milagro, los dos hicieron una suposición correcta, aunque con algunos ingredientes erróneos.

Suponer la homogeneidad limita abruptamente el número de geometrías o espacio-tiempos que se pueden utilizar para describir el universo. Si la materia genera curvatura y si la densidad del fluido cosmológico es la misma en todas partes, la curvatura del universo también debe ser la misma en todas partes. Quedan descartadas así las formas curvas irregulares o estrafalarias: por ejemplo, el universo no puede tener la forma de un elefante, bestia que está muy lejos de ser homogénea. Nos quedan, en realidad, sólo tres posibilidades.

La más sencilla es un espacio tridimensional que no tiene curvatura: el espacio euclidiano. Para ayudar a imaginar los otros dos casos, en la figura 1.a he dibujado un símil bidimensional de un espacio tridimensional real, una hoja plana infinita. Al lector quizá lo sorprenda saber que semejante superficie plana es una de las posibilidades, dado que la materia genera curvatura; pero debe recordar que la materia curva el espacio-tiempo, y no hemos considerado todavía cómo opera el tiempo en este universo.

Veamos cómo abordó Friedmann la cuestión del tiempo. Primero postuló que
todas
las distancias medidas sobre la hoja plana debían multiplicarse por el factor de escala o de expansión del universo. Es posible que el factor varíe con el transcurso del tiempo, lo que daría origen a una dinámica temporal en semejante universo. El modelo de espacio-tiempo correspondiente, entonces, es ese ente combinado: la superficie más un factor de escala que depende del tiempo, entidad que se curva por acción de la materia según las ecuaciones de campo de Einstein. En efecto, cuando Friedmann introdujo esta geometría en las ecuaciones de campo, halló que la entidad es curva. En la figura 2 he graficado el factor de escala en función del tiempo para ese universo.

Se puede observar en la figura que el factor de escala de un universo de geometría plana aumenta con el tiempo, aunque la tasa de incremento disminuye. Esa disminución puede interpretarse como la curvatura del espacio-tiempo. Como veremos más adelante, el destino de semejante universo es excepcional. Si miramos más atentamente la figura 2, veremos que se expande eternamente y que su velocidad de expansión disminuye gradualmente pero jamás se detiene del todo.

Los otros dos espacios son más complejos. Uno de ellos corresponde a la esfera [superficie esférica]
[16]
, que tiene curvatura idéntica en todos sus puntos. Parece algo fácil de imaginar, pero recordemos que estamos hablando de una superficie esférica tridimensional [de una esfera de cuatro dimensiones], no de su equivalente bidimensional. He creado una versión para jardín de infantes en la figura 1.b; si el lector puede "ver" cómo es, lo felicito; yo no puedo, pero no por ello he dejado de trabajar con superficies esféricas tridimensionales. Esa es la ventaja de las matemáticas; nos permiten jugar con objetos que nuestro cerebro no puede imaginar.

Si las esferas tridimensionales son desconcertantes, el tercer tipo de espacio homogéneo lo es aún en mayor grado. Se lo llama seudoesfera o universo abierto. En la figura 1.c he trazado un fragmento de su símil bidimensional; se trata de una superficie infinita en forma de silla de montar. Para contribuir a la comprensión de la seudoesfera, en la figura 3 he usado un artilugio: las secciones trazadas son ortogonales entre sí. En una superficie esférica, en los dos casos se obtiene una circunferencia, razón por la cual se dice a veces incorrectamente que la superficie esférica es el producto de dos circunferencias. Lo mismo ocurre con la seudoesfera, sólo que en ese caso la curvatura de las dos secciones es opuesta. Por eso decimos que esa superficie tiene curvatura negativa, mientras que la superficie esférica habitual tiene curvatura positiva. Así, según la curvatura de las dos secciones, el espacio será finito (como en una superficie esférica) o infinito (como en la seudoesfera).

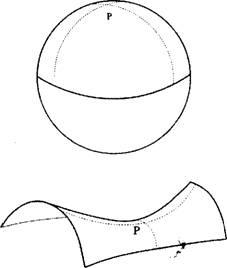
Figura 5 (a) Si trazamos do secciones ortogonales por cualquier punto (P) de una superficie esférica se generan dos circunferencias que se curvan en la misma dirección (en este caso, hacia abajo). (b) La misma operación aplicada a la superficie de una hiperesfera genera dos líneas que se curvan en direcciones opuestas (una de ellas se curva hacia arriba y la otra hacia abajo.

A fin de indicar cómo se combinan estas dos superficies con el tiempo para generar un espacio-tiempo, debemos multiplicar todas sus distancias por un factor de escala o de expansión, que puede depender del tiempo. Cuando Friedmann aplicó esas geometrías a la ecuación de campo de Eins-tein y estudió la evolución del factor de expansión, descubrió que esos espacios tienen un destino aciago, a diferencia del modelo de geometría plana descripto anteriormente. Comprobó que el universo esférico se expande a partir de un
big bang
pero finalmente se detiene y comienza a contraerse para acabar en un
big crunch.
En cambio, el universo correspondiente a la seudoesfera se expande también a partir de un
big bang
pero jamás cesa de expandirse: a diferencia de lo que sucede en el modelo de geometría plana, la desaceleración de la expansión no continúa en él indefinidamente sino que alcanza un ritmo estable. En la figura 2 se grafica la evolución del factor de escala en función del tiempo según Friedmann para los tres modelos posibles.

Nos hemos encontrado antes con la misma antítesis, que no refleja más que una tensión que ya hemos debatido: la guerra entre la expansión y la atracción gravitatoria, o el hecho de que, por un lado, el espacio "se infla" y, por el otro, la fuerza de la gravedad actúa en sentido contrario, empujando todo hacia adentro y tendiendo a congregarlo. La evolución del modelo cerrado o esférico es tal que la gravedad finalmente supera la expansión, de modo que esta última prosigue aunque permanentemente desacelerada por la gravedad, hasta que por fin se detiene y precipita al universo en una contracción cada vez más rápida que termina en el colapso final. En los modelos abiertos o seudoesféricos, por el contrario, la expansión gana la batalla, y el universo acaba por escapar a su propia gravedad. Durante algún tiempo, la gravedad tiene intensidad suficiente para desacelerar la expansión, pero al final, la expansión es tan veloz —o, según otro punto de vista, la materia del universo ha quedado tan diluida— que la gravedad ya no tiene importancia. Por esa razón, la expansión ya no se frena y comienza una fase en la cual el universo "escapa de sí mismo" y se transforma en algo vacío.

Una delgada línea separa a esos dos polos: el modelo de geometría plana —un modelo de mesura británica podríamos decir—, en el cual se produce un equilibrio perfecto entre la expansión y la gravedad. La expansión nunca se libra del todo de la gravedad, pero la gravedad jamás consigue detener la expansión y causar un colapso. El universo se expande por toda la eternidad con verdadera flema y moderación, sin ceder ante la gravedad que lo precipitaría en una implosión catastrófica y sin abandonarse a la expansión descontrolada y el posterior vacío, evitando así con gran sensatez el cataclismo o la muerte, para seguir viviendo hasta alcanzar una edad avanzada y venerable.

La longevidad de los modelos de geometría plana es crucial, pues sólo esos universos viven el tiempo necesario para que la materia se aglutine formando estrellas y galaxias, y para que las escalas de tiempo sean tan grandes que permitan la formación de estructuras y de vida. Puesto que no podemos acelerar el lento proceso por el cual la selección natural genera la inteligencia, sólo hay un tipo de modelo que garantiza el tiempo necesario para que ella actúe sin peligro de una hecatombe cósmica.

Ahora bien, los modelos planos son intrínsecamente inestables porque dependen de un precario equilibrio entre el movimiento cósmico y la gravedad; por milagro, evitan dos finales igualmente catastróficos. La menor desviación de la planitud implica que el espacio-tiempo se cierra sobre sí mismo o se transforma en una superficie tipo silla de montar y se vacía. En cualquiera de los dos casos, se precipita vertiginosamente hacia la muerte. De hecho, parecería entonces que el universo ha estado caminando sobre una cuerda floja durante 15 mil millones de años, algo sumamente improbable, si no francamente imposible. Esto se conoce como
problema de la planitud
, segundo enigma del
big bang
que ha acosado a los cosmólogos desde que Friedmann develó el panorama de la cosmología relativista.

Existe una descripción posible de esta pulseada, un número que se llama Omega (como la letra griega). Omega es aproximadamente igual al cociente entre la energía gravitatoria del universo y la energía implícita en su movimiento de expansión. En el universo de geometría plana, ambas cantidades son iguales en todo momento, de modo que Omega es igual a uno. En los modelos cerrados, Omega es mayor que uno pues su energía gravitatoria es mayor que su energía cinética; en los modelos abiertos, Omega es menor que uno.

Omega se puede expresar de una manera equivalente, definiendo, para una velocidad de expansión determinada, la densidad de materia que genera la cantidad exacta de energía gravitatoria necesaria para equilibrar la energía de expansión. Esta densidad se denomina
crítica
, siguiendo la nomenclatura de las armas nucleares. Es la densidad necesaria para que Omega sea igual a 1 permanentemente, es decir, necesaria para la planitud. Si la densidad cósmica supera este valor crítico, la gravedad gana la partida y nos hallamos frente a un modelo cerrado. Por el contrario, si la densidad es menor que el valor crítico, tenemos la certeza de que en ausencia de gravedad el universo acabará por "escapar de sí mismo" mediante una explosión, y nos hallamos frente a un modelo abierto. No sorprende pues que Omega se pueda expresar como el cociente entre la densidad cósmica real y la densidad crítica, y que ese valor describa el estado actual de ese gigantesco tira y afloja.

El problema de la planitud es tan poco dócil a cualquier tratamiento porque, a medida que el universo se expande, las desviaciones del valor 1 de Omega aumentan abruptamente, como se puede ver en la figura 4. En el modelo de geometría plana, Omega es igual a uno eternamente, pero el menor exceso de un tipo de energía sobre el otro, es decir, la menor diferencia entre la densidad cósmica real y la crítica genera una situación que sólo puede empeorar y que, de hecho, empeora rápidamente.

El padre del universo inflacionario, Alan Guth, cuenta que ese problema lo obsesionaba en los meses anteriores a su gran descubrimiento. Tenía entonces poco más de treinta años y estaba en un momento decisivo de su carrera, de modo que no tenía por qué preocuparse por la cosmología, que en ese entonces no era una rama respetable de la física. Se la veía como una empresa que cualquier joven científico debía evitar como si fuera la peste, dejándola en manos de hombres más maduros, víctimas de atrofia cerebral.
[17]

Guth sufría presiones para publicar rápidamente aburridos trabajos encuadrados dentro de las principales tendencias imperantes en la física, pero hubo una serie de casualidades que lo hicieron asistir a una conferencia que dio en Cornell el famoso físico Robert Dicke, quien expuso allí el problema de la planitud.

Dicke impresionó mucho al auditorio expresando numéricamente el problema. Así, mostró que cuando el universo tenía sólo un segundo de edad, el valor de Omega debió estar comprendido entre 0,99999999999999999 y 1,00000000000000001. Si Omega hubiera estado fuera de ese rango, el universo se habría precipitado en el vacío o en un colapso total y no estaríamos aquí para debatir una cuestión filosófica tan fundamental. Ese comentario impresionó de tal manera a Guth, que cambió el rumbo de su carrera y terminó formulando la teoría inflacionaria. ¿A qué se debía un ajuste tan fino de Omega?