Data Mining (34 page)
Authors: Mehmed Kantardzic

Each training (learning) sample with two inputs and one output value (x
1
, x
2
, o) removes half the hypotheses (h
i
). For example, sample (0, 0, 0) removes h
9
to h
16
because these hypotheses have output value 1 for the input pair (0, 0). This is one way of interpreting learning: We start with all possible hypotheses, and as we see more training samples we remove non-consistent hypotheses. After seeing N samples, there remain 2
2d-N
possible hypotheses, that is, Boolean functions as a model for a given data set. In reality, where all inputs are usually not binary but with k different values (k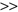 ), and also data are high-dimensional (d
), and also data are high-dimensional (d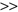 ), then k
), then k
d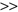 N. The number of samples for real-world data is significantly lower than the number of hypotheses (or the number of potential models). Therefore, data set by itself is not sufficient to find a unique solution—model. There is still huge number of hypotheses. We have to make some extra assumptions to reach a unique solution with the given data (N samples). These assumptions we call inductive bias (principle) of the learning algorithm. It influences a model selection. The main question is: How well does a model trained on training data set predict the right output for new samples (not available in training data). This represents an essential requirement for model generalization. For best generalization, we should match the complexity of the hypothesis class with the complexity of the function underlying training data. We made in the learning process a trade-off between the complexity of the hypothesis, the amount of data, and the generalization error of new samples (Fig.
N. The number of samples for real-world data is significantly lower than the number of hypotheses (or the number of potential models). Therefore, data set by itself is not sufficient to find a unique solution—model. There is still huge number of hypotheses. We have to make some extra assumptions to reach a unique solution with the given data (N samples). These assumptions we call inductive bias (principle) of the learning algorithm. It influences a model selection. The main question is: How well does a model trained on training data set predict the right output for new samples (not available in training data). This represents an essential requirement for model generalization. For best generalization, we should match the complexity of the hypothesis class with the complexity of the function underlying training data. We made in the learning process a trade-off between the complexity of the hypothesis, the amount of data, and the generalization error of new samples (Fig.
4.31
). Therefore, building a data-mining model is not a straightforward procedure, but a very sensitive process requiring, in many cases, feedback information for multiple mining iterations.
Figure 4.31.
Trade-off between model complexity and the amount of data. (a) Too simple model; (b) too complex model; (c) appropriate model.
In the final phase of the data-mining process, when the model is obtained using one or more inductive-learning techniques, one important question still exists. How does one verify and validate the model? At the outset, let us differentiate between
validation
and
verification.
Model
validation
is substantiating that the model, within its domain of applicability, behaves with satisfactory accuracy consistent with the objectives defined by the users. In other words, in model validation, we substantiate that the data have transformed into the model and that they have sufficient accuracy in representing the observed system. Model validation deals with building the
right
model, the model that corresponds to the system. Model
verification
is substantiating that the model is transformed from the data as intended into new representations with sufficient accuracy. Model verification deals with building the model
right,
the model that corresponds correctly to the data.
Model validity is a necessary but insufficient condition for the credibility and acceptability of data-mining results. If, for example, the initial objectives are incorrectly identified or the data set is improperly specified, the data-mining results expressed through the model will not be useful; however, we may still find the model valid. We can claim that we conducted an “excellent” data-mining process, but the decision makers will not accept our results and we cannot do anything about it. Therefore, we always have to keep in mind, as it has been said, that a problem correctly formulated is a problem half-solved. Albert Einstein once indicated that the correct formulation and preparation of a problem was even more crucial than its solution. The ultimate goal of a data-mining process should not be just to produce a model for a problem at hand, but to provide one that is sufficiently credible and accepted and implemented by the decision makers.
The data-mining results are validated and verified by the testing process. Model testing is demonstrating that inaccuracies exist or revealing the existence of errors in the model. We subject the model to test data or test cases to see if it functions properly. “Test failed” implies the failure of the model, not of the test. Some tests are devised to evaluate the behavioral accuracy of the model (i.e., validity), and some tests are intended to judge the accuracy of data transformation into the model (i.e., verification).
The objective of a model obtained through the data-mining process is to classify/predict new instances correctly. The commonly used measure of a model’s quality is predictive accuracy. Since new instances are not supposed to be seen by the model in its learning phase, we need to estimate its predictive accuracy using the true error rate. The true error rate is statistically defined as the error rate of the model on an asymptotically large number of new cases that converge to the actual population distribution. In practice, the true error rate of a data-mining model must be estimated from all the available samples, which are usually split into training and testing sets. The model is first designed using training samples, and then it is evaluated based on its performance on the test samples. In order for this error estimate to be reliable in predicting future model performance, not only should the training and the testing sets be sufficiently large, they must also be independent. This requirement of independent training and test samples is still often overlooked in practice.
How should the available samples be split to form training and test sets? If the training set is small, then the resulting model will not be very robust and will have low generalization ability. On the other hand, if the test set is small, then the confidence in the estimated error rate will be low. Various methods are used to estimate the error rate. They differ in how they utilize the available samples as training and test sets. If the number of available samples is extremely large (say, 1 million), then all these methods are likely to lead to the same estimate of the error rate. If the number of samples is smaller, then the designer of the data-mining experiments has to be very careful in splitting the data. There are no good guidelines available on how to divide the samples into subsets. No matter how the data are split, it should be clear that different random splits, even with the specified size of training and testing sets, would result in different error estimates.
Let us discuss different techniques, usually called
resampling methods
, for splitting data sets into training and test samples. The main advantage of using the resampling approach over the analytical approach for estimating and selecting models is that the former does not depend on assumptions about the statistical distribution of the data or specific properties of approximating functions. The main disadvantages of resampling techniques are their high computational effort and the variation in estimates depending on the resampling strategy.
The basic approach in model estimation is first to prepare or to learn a model using a portion of the training data set and then to use the remaining samples to estimate the prediction risk for this model. The first portion of the data is called a learning set, and the second portion is a validation set, also called a testing set. This
naïve strategy
is based on the assumption that the learning set and the validation set are chosen as representatives of the same, unknown distribution of data. This is usually true for large data sets, but the strategy has an obvious disadvantage for smaller data sets. With a smaller number of samples, the specific method of splitting the data starts to have an impact on the accuracy of the model. The various methods of resampling are used for smaller data sets, and they differ according to the strategies used to divide the initial data set. We will give a brief description of the resampling methods that are common in today’s data-mining practice, and a designer of a data-mining system will have to make a selection based on the characteristics of the data and the problem.
1.
Resubstitution Method.
This is the simplest method. All the available data are used for training as well as for testing. In other words, the training and testing sets are the same. Estimation of the error rate for this “data distribution” is optimistically biased (estimated error is often smaller than could be expected in real applications of the model), and therefore the method is very seldom used in real-world data-mining applications. This is especially the case when the ratio of sample size to dimensionality is small.
2.
Holdout Method
.
Half the data, or sometimes two-thirds of the data, is used for training and the remaining data are used for testing. Training and testing sets are independent and the error estimation is pessimistic. Different partitioning will give different estimates. A repetition of the process, with different training and testing sets randomly selected, and integration of the error results into one standard parameter, will improve the estimate of the model.
3.
Leave-One-Out Method
.
A model is designed using (n − 1) samples for training and evaluated on the one remaining sample. This is repeated n times with different training sets of size (n − 1). This approach has large computational requirements because n different models have to be designed and compared.
4.
Rotation Method (n-Fold Cross-Validation).
This approach is a compromise between holdout and leave-one-out methods. It divides the available samples into P disjoint subsets, where 1 ≤ P ≤ n. (P − 1) subsets are used for training and the remaining subset for testing. This is the most popular method in practice, especially for problems where the number of samples is relatively small.
5.
Bootstrap Method.
This method resamples the available data with replacements to generate a number of “fake” data sets of the same size as the given data set. The number of these new sets is typically several hundreds. These new training sets can be used to define the so-called bootstrap estimates of the error rate. Experimental results have shown that the bootstrap estimates can outperform the cross-validation estimates. This method is especially useful in small data set situations.