To Explain the World: The Discovery of Modern Science (40 page)

(
a
)     
N
= 3 ,     
n
= 3

(
b
)     
N
= 4 ,     
n
= 3

(
c
)     
N
= 5 ,     
n
= 3

(
d
)     
N
= 3 ,     
n
= 4

(e)     
N
= 3 ,     
n
= 5

(In the cases
n
= 3,
n
= 4, and
n
= 5 the sides of the regular polyhedron are respectively equilateral triangles, squares, and regular pentagons.) These are the values of
N
and
n
that we find in the tetrahedron, octahedron, icosahedron, cube, and dodecahedron.

This much was proved by Euclid. But Euclid did not prove that there is only one regular polyhedron for each pair of
n
and
N.
In what follows, we will go beyond Euclid, and show that for each value of
N
and
n
we can find unique results for the other properties of the polyhedron: the number
F
of faces, the number
E
of edges, and the number
V
of vertices. There are three unknowns here, so for this purpose we need three equations. To derive the first, note that the total number of borders of all the polygons on the surface of the polyhedron is
nF
, but each of the
E
edges borders two polygons, so

2
E
=
nF

Also, there are
N
edges coming together at each of the
V
vertices, and each of the
E
edges connects two vertices, so

2
E
=
NV

Finally, there is a more subtle relation among
F
,
E
, and
V.
In deriving this relation, we must make an additional assumption, that the polyhedron is simply connected, in the sense that any path
between two points on the surface can be continuously deformed into any other path between these points. This is the case for instance for a cube or a tetrahedron, but not for a polyhedron (regular or not) constructed by drawing edges and faces on the surface of a doughnut. A deep theorem states that any simply connected polyhedron can be constructed by adding edges, faces, and/or vertices to a tetrahedron, and then if necessary continuously squeezing the resulting polyhedron into some desired shape. Using this fact, we shall now show that any simply connected polyhedron (regular or not) satisfies the relation:

F
−
E
+
V
= 2

It is easy to check that this is satisfied for a tetrahedron, in which case we have
F
= 4,
E
= 6, and
V
= 4, so the left-hand side is 4 – 6 + 4 = 2. Now, if we add an edge to any polyhedron, running across a face from one edge to another, we add one new face and two new vertices, so
F
and
V
increase by one unit and two units, respectively. But this splits each old edge at the ends of the new edge into two pieces, so
E
increases by 1 + 2 = 3, and the quantity
F
–
E
+
V
is thereby unchanged. Likewise, if we add an edge that runs from a vertex to one of the old edges, then we increase
F
and
V
by one unit each, and
E
by two units, so the quantity
F
–
E
+
V
is still unchanged. Finally, if we add an edge that runs from one vertex to another vertex, then we increase both
F
and
E
by one unit each and do not change
V
, so again
F
–
E
+
V
is unchanged. Since any simply connected polyhedron can be built up in this way, all such polyhedrons have the same value for this quantity, which therefore must be the same value
F
–
E
+
V
= 2 as for a tetrahedron. (This is a simple example of a branch of mathematics known as topology; the quantity
F
–
E
+
V
is known in topology as the “Euler characteristic” of the polyhedron.)

We can now solve these three equations for
E
,
F
, and
V.
It is simplest to use the first two equations to replace
F
and
V
in the third equation with 2
E
/
n
and 2
E
/
N
, respectively, so that the third equation becomes 2
E
/
n
–
E
+ 2
E
/
N
= 2, which gives

Then using the other two equations, we have

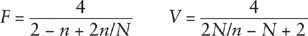
Thus for the five cases listed above, the numbers of faces, vertices, and edges are:

These are the Platonic solids.

3. Harmony

The Pythagoreans discovered that two strings of a musical instrument, with the same tension, thickness, and composition, will make a pleasant sound when plucked at the same time, if the ratio of the strings’ lengths is a ratio of small whole numbers, such as 1/2, 2/3, 1/4, 3/4, etc. To see why this is so, we first need to work out the general relation between the frequency, wavelength, and velocity of any sort of wave.

Any wave is characterized by some sort of oscillating amplitude. The amplitude of a sound wave is the pressure in the air carrying the wave; the amplitude of an ocean wave is the height of the water; the amplitude of a light wave with a definite direction of polarization is the electric field in that direction; and the amplitude of a wave moving along the string of a musical
instrument is the displacement of the string from its normal position, in a direction at right angles to the string.

There is a particularly simple kind of wave known as a sine wave. If we take a snapshot of a sine wave at any moment, we see that the amplitude vanishes at various points along the direction the wave is traveling. Concentrating for a moment on one such point, if we look farther along the direction of travel we will see that the amplitude rises and then falls again to zero, then as we look farther it falls to a negative value and rises again to zero, after which it repeats the whole cycle again and again as we look still farther along the wave’s direction. The distance between points at the beginning and end of any one complete cycle is a length characteristic of the wave, known as its wavelength, and conventionally denoted by the symbol
λ
(lambda). It will be important in what follows that, since the amplitude of the wave vanishes not only at the beginning and end of a cycle but also in the middle, the distance between successive vanishing points is half a wavelength,
λ
/2. Any two points where the amplitude vanishes therefore must be separated by some whole number of half wavelengths.

There is a fundamental mathematical theorem (not made explicit until the early nineteenth century) that virtually any disturbance (that is, any disturbance having a sufficiently smooth dependence on distance along the wave) can be expressed as a sum of sine waves with various wavelengths. (This is known as “Fourier analysis.”)

Each individual sine wave exhibits a characteristic oscillation in time, as well as in distance along the wave’s direction of motion. If the wave is traveling with velocity
v
, then in time
t
it travels a distance
vt.
The number of wavelengths that pass a fixed point in time
t
will thus be
vt
/
λ
, so the number of cycles per second at a given point in which the amplitude and rate of change both keep going back to the same value is
v
/
λ
. This is known as the frequency, denoted by the symbol
ν
(nu), so
ν
=
v
/
λ
. The velocity of a wave of vibration of a string is close to a constant, depending on the string tension and mass, but nearly
independent of its wavelength or its amplitude, so for these waves (as for light) the frequency is simply inversely proportional to the wavelength.

Now consider a string of some musical instrument, with length
L.
The amplitude of the wave must vanish at the ends of the string, where the string is held fixed. This condition limits the wavelengths of the individual sine waves that can contribute to the total amplitude of the string’s vibration. We have noted that the distance between points where the amplitude of any sine wave vanishes can be any whole number of half wavelengths. Thus the wave on a string that is fixed at both ends must contain a whole number
N
of half wavelengths, so that
L
=
Nλ
/2. That is, the only possible wavelengths are
λ
= 2
L
/
N
, with
N
= 1, 2, 3, etc., and so the only possible frequencies are
*

ν
=
vN
/2
L

The lowest frequency, for the case
N
= 1, is
v
/2
L
; all the higher frequencies, for
N
= 2,
N
= 3, etc., are known as the “overtones.” For instance, the lowest frequency of the middle C string of any instrument is 261.63 cycles per second, but it also vibrates at 523.26 cycles per second, 784.89 cycles per second, and so on. The intensities of the different overtones make the difference in the qualities of the sounds from different musical instruments.

Now, suppose that vibrations are set up in two strings that have different lengths
L
₁
and
L
₂
, but are otherwise identical, and in particular have the same wave velocity
v.
In time
t
the modes of vibration of the lowest frequency of the first and second strings will go through
n
₁
=
ν
₁
t
=
vt
/2
L
₁
and
n
₂
=
ν
₂
t
=
vt
/2
L
₂
cycles or fractions of cycles, respectively. The ratio is

n
₁
/
n
₂
=
L
₂
/
L
₁