To Explain the World: The Discovery of Modern Science (43 page)

Next consider a body whose weight is greater than the weight of an equal volume of water. Such a body will not float, but it can be suspended in the water from a cable. If the cable is attached to one arm of a balance, then in this way we can measure the apparent weight
W
_apparent
of the body when submerged in water. The weight pressing down on a horizontal patch in the water at some depth directly below the suspended body will equal the true weight
W
_true
of the suspended body, less the apparent weight
W
_apparent
, which is canceled by the tension in the cable, plus the weight of the water above the patch, which of course does not include the water displaced by the body. We can compare this with the weight pressing down on an equal area at an equal depth, a weight that does not include
W
_true
or –
W
_apparent
, but does include the weight of all the water from this patch to the surface, with no water displaced. In order for both patches to be pressed down by the same weight, we must have

W
_true
−
W
_apparent
=
W
_displaced

where
W
_displaced
is the weight of the water displaced by the suspended body. So by weighing the body when suspended in the water and weighing it when out of the water, we can find both
W
_apparent
and
W
_true
, and in this way find
W
_displaced
. If the body has volume
V
, then

W
_displaced
=
ρ
_water
V

where
ρ
_water
(rho
_water
) is the density (weight per volume) of water, close to 1 gram per cubic centimeter. (Of course, for a body with a simple shape like a cube we could instead find
V
by just measuring the dimensions of the body, but this is difficult for an irregularly shaped body like a crown.) Also, the true weight of the body is

W
_true
=
ρ
_body
V

where
ρ
_body
is the density of the body. The volume cancels in the ratio of
W
_true
and
W
_displaced
, so from the measurements of both
W
_apparent
and
W
_true
we can find the ratio of the densities of the body and of water:

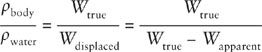
This ratio is called the “specific gravity” of the material of which the body is composed. For instance, if the body weighs 20 percent less in water than in air, then
W
_true
–
W
_apparent
= 0.20 ×
W
_true
, so its density must be 1/0.2 = 5 times the density of water. That is, its specific gravity is 5.

There is nothing special about water in this analysis; if the same measurements were made for a body suspended in some other liquid, then the ratio of the true weight of the body to the decrease in its weight when suspended in the liquid would give the ratio of the density of the body to the density of that liquid. This relation is sometimes used with a body of known weight
and volume to measure the densities of various liquids in which the body may be suspended.

10. Areas of Circles

To calculate the area of a circle, Archimedes imagined that a polygon with a large number of sides was circumscribed outside the circle. For simplicity, let’s consider a regular polygon, all of whose sides and angles are equal. The area of the polygon is the sum of the areas of all the right triangles formed by drawing lines from the center to the corners of the polygon, and lines from the center to the midpoints of the sides of the polygon. (See Figure 4, in which the polygon is taken to be a regular octagon.) The area of a right triangle is half the product of its two sides around the right angle, because two such triangles can be stacked on their hypotenuses to make a rectangle, whose area is the product of the sides. In our case, this means that the area of each triangle is half the product of the distance
r
to the midpoint of the side (which is just the radius of the circle) and the distance
s
from the midpoint of the side to the nearest corner of the polygon, which of course is half the length of that side of the polygon. When we add up all these areas, we find that the area of the whole polygon equals half of
r
times the total circumference of the polygon. If we let the number of sides of the polygon become infinite, its area approaches the area of the circle, and its circumference approaches the circumference of the circle. So the area of the circle is half its circumference times its radius.

In modern terms, we define a number
π
= 3.14159 . . . such that the circumference of a circle of radius
r
is 2
πr
. The area of the circle is thus

1/2 ×
r
× 2
πr
=
πr
²

The same argument works if we inscribe polygons within the circle, rather than circumscribing them outside the circle as in Figure 4. Since the circle is always between an outer polygon circumscribed around it and an inner polygon inscribed within it, using polygons of both sorts allowed Archimedes to give upper and lower limits for the ratio of the circumference of a circle to its radius—in other words, for 2
π
.

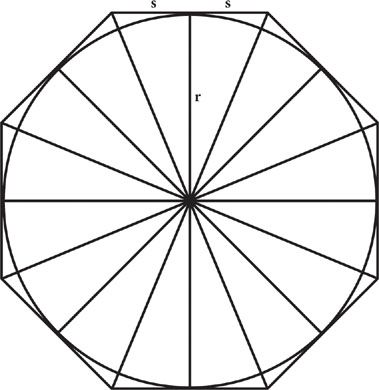
Figure 4. Calculation of the area of a circle.
In this calculation a polygon with many sides is circumscribed about a circle. Here, the polygon has eight sides, and its area is already close to the area of the circle. As more sides are added to the polygon, its area becomes closer and closer to the area of the circle.

11. Sizes and Distances of the Sun and Moon

Aristarchus used four observations to determine the distances from the Earth to the Sun and Moon and the diameters of the Sun and Moon, all in terms of the diameter of the Earth. Let’s
look at each observation in turn, and see what can be learned from it. Below,
d
_s
and
d
_m
are the distances from the Earth to the Sun and Moon, respectively; and
D
_s
,
D
_m
, and
D
_e
denote the diameters of the Sun, Moon, and Earth. We will assume that the diameters are negligible compared with the distances, so in talking of the distance from the Earth to the Moon or Sun, it is unnecessary to specify points on the Earth, Moon, or Sun from which the distances are measured.

Observation 1

When the Moon is half full, the angle between the lines of sight from the Earth to the Moon and to the Sun is 87°.

When the Moon is half full, the angle between the lines of sight from the Moon to the Earth and from the Moon to the Sun must be just 90° (see Figure 5a), so the triangle formed by the lines Moon–Sun, Moon–Earth, and Earth–Sun is a right triangle, with the Earth–Sun line as the hypotenuse. The ratio between the side adjacent to an angle
θ
(theta) of a right triangle and the hypotenuse is a trigonometric quantity known as the cosine of
θ
, abbreviated cos
θ
, which we can look up in tables or find on any scientific calculator. So we have

d
_m
/
d
_s
= cos 87° = 0.05234 = 1/19.11

and this observation indicates that the Sun is 19.11 times farther from the Earth than is the Moon. Not knowing trigonometry, Aristarchus could only conclude that this number is between 19 and 20. (The angle actually is not 87°, but 89.853°, and the Sun is really 389.77 times farther from the Earth than is the Moon.)

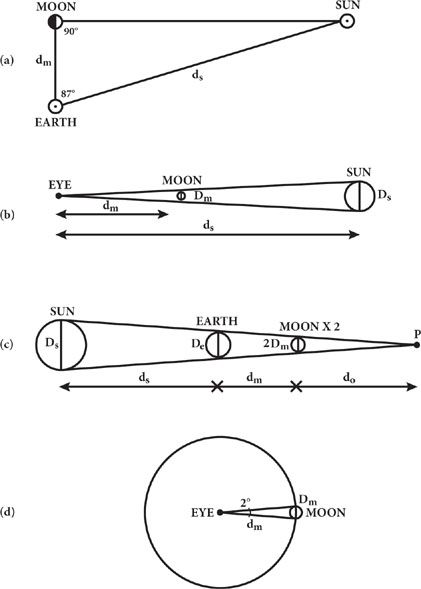
Figure 5. The four observations used by Aristarchus to calculate the sizes and distances of the Sun and Moon.
(a) The triangle formed by the Earth, Sun, and Moon when the Moon is half full. (b) The Moon just blotting out the disk of the Sun during a total eclipse of the Sun. (c) The Moon passing into the shadow of the Earth during an eclipse of the Moon. The sphere that just fits into this shadow has a diameter twice that of the Moon, and
P
is the terminal point of the shadow cast by the Earth. (d) Lines of sight to the Moon spanning an angle of 2°; the actual angle is close to 0.5°.

Observation 2

The Moon just covers the visible disk of the Sun during a solar eclipse.

This shows that the Sun and Moon have essentially the same apparent size, in the sense that the angle between the lines of sight from the Earth to opposite sides of the disk of the Sun is the same as for the Moon. (See Figure 5b.) This means that the triangles formed by these two lines of sight and the diameters of the Sun and Moon are “similar”; that is, they have the same shape. Hence the ratios of corresponding sides of these two triangles are the same, so

D
_s
/
D
_m
=
d
_s
/
d
_m

Using the result of observation 1 then gives
D
_s
/
D
_m
= 19.11, while the actual ratio of diameters is really close to 390.

Observation 3

The shadow of the Earth at the position of the Moon during a lunar eclipse is just wide enough to fit a sphere with twice the diameter of the Moon.

Let
P
be the point where the cone of shadow cast by the Earth ends. Then we have three similar triangles: the triangle formed by the diameter of the Sun and the lines from the edges of the Sun’s disk to
P
; the triangle formed by the diameter of the Earth and the lines from the edges of the Earth’s disk to
P
; and the triangle formed by twice the diameter of the Moon and the lines from a sphere with that diameter at the position of the Moon during a lunar eclipse to
P.
(See Figure 5c.) It follows that the ratios of corresponding sides of these triangles are all equal. Suppose that point
P
is at distance
d
₀
from the Moon. Then the Sun is at distance
d
_s
+
d
_m
+
d
₀
from
P
and the Earth is at distance
d
_m
+
d
₀
from
P
, so