To Explain the World: The Discovery of Modern Science (45 page)

12. The Size of the Earth

Eratosthenes used the observation that at noon on the summer solstice, the Sun at Alexandria is 1/50 of a full circle (that is, 360°/50 = 7.2°) away from the vertical, while at Syene, a city supposedly due south of Alexandria, the Sun at noon on the summer solstice was reported to be directly overhead. Because the Sun is so far away, the light rays striking the Earth at Alexandria and Syene are essentially parallel. The vertical direction at any city is just the continuation of a line from the center of the Earth to that city, so the angle between the lines from the Earth’s center to Syene and to Alexandria must also be 7.2°, or 1/50 of a full circle. (See Figure 6.) Hence on the basis of the assumptions of Eratosthenes, the Earth’s circumference must be 50 times the distance from Alexandria to Syene.

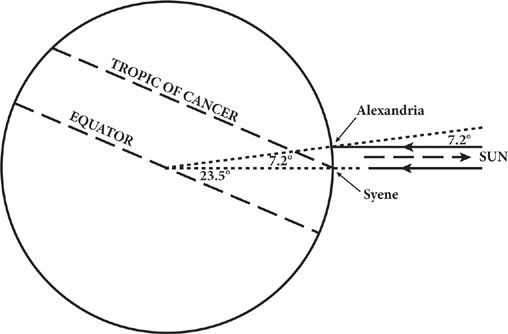
Figure 6. The observation used by Eratosthenes to calculate the size of the Earth.
The horizontal lines marked with arrows indicate rays of sunlight at the summer solstice. The dotted lines run from the Earth’s center to Alexandria and Syene, and mark the vertical direction at each place.

Syene is not on the Earth’s equator, as might be suggested by the way the figure is drawn, but rather close to the Tropic of Cancer, the line at latitude 231⁄2°. (That is, the angle between lines from the Earth’s center to any point on the Tropic of Cancer and to a point due south on the equator is 231⁄2°.) At the summer solstice the Sun is directly overhead at noon on the Tropic of Cancer rather than on the equator because the Earth’s axis of rotation is not perpendicular to the plane of its orbit, but tilted from the perpendicular by an angle of 231⁄2°.

13. Epicycles for Inner and Outer Planets

Ptolemy in the
Almagest
presented a theory of the planets according to which, in its simplest version, each planet goes on a circle called an epicycle around a point in space that itself goes around the Earth on a circle known as the planet’s deferent. The question before us is why this theory worked so well in accounting for the apparent motions of the planets as seen from Earth. The answer for the inner planets, Mercury and Venus, is different from that for the outer planets, Mars, Jupiter, and Saturn.

First, consider the inner planets, Mercury and Venus. According to our modern understanding, the Earth and each planet go around the Sun at approximately constant distances from the Sun and at approximately constant speeds. If we do not concern ourselves with the laws of physics, we can just as well change our point of view to one centered on the Earth. From this point of view, the Sun goes around the Earth, and each planet goes around the Sun, all at constant speeds and distances. This is a simple version of the theory due to Tycho Brahe, which may also have been proposed by Heraclides. It gives the correct apparent motions of the planets, apart from small corrections due to the facts that planets actually move on nearly circular elliptical orbits rather than on circles, the Sun is not at the centers of these ellipses but at relatively small distances from the centers, and the speed of each planet varies somewhat as the planet goes around its orbit. It is also a special case of the theory of Ptolemy, though one never considered by Ptolemy, in which the deferent is nothing but the orbit of the Sun around the Earth, and the epicycle is the orbit of Mercury or Venus around the Sun.

Now, as far as the apparent position in the sky of the Sun and planets is concerned, we can multiply the changing distance of any planet from the Earth by a constant, without changing appearances. This can be done, for instance, by multiplying the radii of both the epicycle and the deferent by the same constant factor, chosen independently for Mercury and Venus. For instance, we could take the radius of the deferent of Venus to be half the
distance of the Sun from the Earth, and the radius of its epicycle to be half the radius of the orbit of Venus around the Sun. This will not change the fact that the centers of the planets’ epicycles always stay on the line between the Earth and the Sun. (See Figure 7a, which shows the epicycle and deferent for one of the inner planets, not drawn to scale.) The apparent motion of Venus and Mercury in the sky will be unchanged by this transformation, as long as we don’t change the ratio of the radii of each planet’s deferent and epicycle. This is a simple version of the theory proposed by Ptolemy for the inner planets. According to this theory, the planet goes around its epicycle in the same time that it actually takes to go around the Sun, 88 days for Mercury and 225 days for Venus, while the center of the epicycle follows the Sun around the Earth, taking one year for a complete circuit of the deferent.

Specifically, since we do not change the ratio of the radii of the deferent and epicycle, we must have

r
_EPI
/
r
_DEF
=
r
_P
/
r
_E

where
r
_EPI
and
r
_DEF
are the radii of the epicycle and deferent in Ptolemy’s scheme, and
r
_P
and
r
_E
are the radii of the orbits of the planet and the Earth in the theory of Copernicus (or equivalently, the radii of the orbits of the planet around the Sun and the Sun around the Earth in the theory of Tycho). Of course, Ptolemy knew nothing of the theories of Tycho or Copernicus, and he did not obtain his theory in this way. The discussion above serves to show only why Ptolemy’s theory worked so well, not how he derived it.

Now, let us consider the outer planets, Mars, Jupiter, and Saturn. In the simplest version of the theory of Copernicus (or Tycho) each planet keeps a fixed distance not only from the Sun, but also from a moving point
C
ʹ in space, which keeps a fixed distance from the Earth. To find this point, draw a parallelogram (Figure 7b), whose first three vertices in order around it are the position
S
of the Sun, the position
E
of the Earth, and the position
Pʹ
of one of the planets. The moving point
Cʹ
is the empty
fourth corner of the parallelogram. Since the line between
E
and
S
has a fixed length, and the line between
Pʹ
and
Cʹ
is the opposite side of the parallelogram, it has an equal fixed length, so the planet stays at a fixed distance from
Cʹ
, equal to the distance of the Earth from the Sun. Likewise, since the line between
S
and
pʹ
has a fixed length, and the line between
E
and
Cʹ
is the opposite side of the parallelogram, it has an equal fixed length, so point
Cʹ
stays at a fixed distance from the Earth, equal to the distance of the planet from the Sun. This is a special case of the theory of Ptolemy, though a case never considered by him, in which the deferent is nothing but the orbit of point
Cʹ
around the Earth, and the epicycle is the orbit of Mars, Jupiter, or Saturn around
Cʹ
.

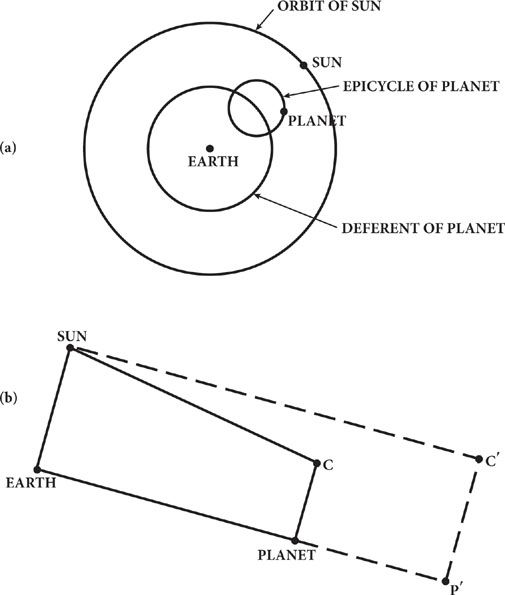
Figure 7. A simple version of the epicycle theory described by Ptolemy.
(a) The supposed motion of one of the inner planets, Mercury or Venus. (b) The supposed motion of one of the outer planets Mars, Jupiter, or Saturn. Planet
P
goes on an epicycle around point
C
in one year, with the line from
C
to
P
always parallel to the line from the Earth to the Sun, while point
C
goes around the Earth on the deferent in a longer time. (The dashed lines indicate a special case of the Ptolemaic theory, for which it is equivalent to that of Copernicus.)

Once again, as far as the apparent position in the sky of the Sun and planets is concerned, we can multiply the changing distance of any planet from the Earth by a constant without changing appearances, by multiplying the radii of both the epicycle and the deferent by a constant factor, chosen independently for each outer planet. Although we no longer have a parallelogram, the line between the planet and
C
remains parallel to the line between the Earth and Sun. The apparent motion of each outer planet in the sky will be unchanged by this transformation, as long as we don’t change the ratio of the radii of each planet’s deferent and epicycle. This is a simple version of the theory proposed by Ptolemy for the outer planets. According to this theory, the planet goes around
C
on its epicycle in 1 year, while
C
goes around the deferent in the time that it actually takes the planet to go around the Sun: 1.9 years for Mars, 12 years for Jupiter, and 29 years for Saturn.

Specifically, since we do not change the ratio of the radii of the deferent and epicycle, we must now have

r
_EPI
/
r
_DEF
=
r
_E
/
r
_P

where
r
_EPI
and
r
_DEF
are again the radii of the epicycle and deferent in Ptolemy’s scheme, and
r
_P
and
r
_E
are the radii of the orbits of
the planet and the Earth in the theory of Copernicus (or equivalently, the radii of the orbits of the planet around the Sun and the Sun around the Earth in the theory of Tycho). Once again, the above discussion describes, not how Ptolemy obtained his theory, but only why this theory worked so well.

14. Lunar Parallax

Suppose that the direction to the Moon is observed from point
O
on the surface of the Earth to be at angle
ζʹ
(zeta prime) to the zenith at
O.
The Moon moves in a smooth and regular way around the center of the Earth, so by using the results of repeated observations of the Moon it is possible to calculate the direction from the center
C
of the Earth to the Moon
M
at the same moment, and in particular to calculate angle
ζ
between the direction from
C
to the Moon and the direction of the zenith at
O
, which is the same as the direction of the line from the center of the Earth to
O.
Angles
ζ
and
ζʹ
differ slightly because the radius
r
_e
of the earth is not entirely negligible compared with the distance
d
of the Moon from the center of the Earth, and from this difference Ptolemy could calculate the ratio
d
/
r
_e
.

Points
C
,
O
, and
M
form a triangle, in which the angle at
C
is
ζ
, the angle at
O
is 180° –
ζʹ
, and (since the sum of the angles of any triangle is 180°) the angle at
M
is 180° –
ζ
– (180° –
ζʹ
) =
ζʹ
–
ζ
. (See Figure 8.) We can calculate the ratio
d
/
r
_e
from these angles much more easily than Ptolemy did, by using a theorem of modern trigonometry: that in any triangle the lengths of sides are proportional to the sines of the opposite angles. (Sines are discussed in Technical Note 15.) The angle opposite the line of length
r
_e
from
C
to
O
is
ζʹ
–
ζ
, and the angle opposite the line of length
d
from
C
to
M
is 180° –
ζʹ
, so