To Explain the World: The Discovery of Modern Science (49 page)

where
β
(beta) and
γ
(gamma) are two more numbers, which respectively specify the tilt and height of the plane. (We are defining the coordinates so that the plane is parallel to the
y
-axis.) Combining Eq. (9) with the square of Eq. (8) gives

u
²
+
y
²
=
α
²
(
βu
+
γ
)
²

or equivalently

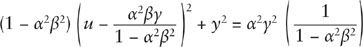
This is the same as the defining Eq. (1) if we identify

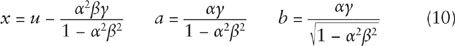
Note that this gives
e
=
αβ
, so the eccentricity depends on the shape of the cone and on the tilt of the plane cutting the cone, but not on the plane’s height.

19. Elongations and Orbits of the Inner Planets

One of the great achievements of Copernicus was to work out definite values for the relative sizes of planetary orbits. A particularly simple example is the calculation of the radii of the orbits of the inner planets from the maximum apparent distance of these planets from the Sun.

Consider the orbit of one of the inner planets, Mercury or Venus, in the approximation that it and the Earth’s orbit are both circles with the Sun at the center. At what is called “maximum
elongation,” the planet is seen at the greatest angular distance
θ
_max
(theta
_max
) from the Sun. At this time, the line from the Earth to the planet is tangent to the planet’s orbit, so the angle between this line and the line between the Sun and the planet is a right angle. These two lines and the line from the Sun to the Earth thus form a right triangle. (See Figure 13.) The hypotenuse of this triangle is the line between the Earth and the Sun, so the ratio of the distance
r
_P
between the planet and the Sun to the distance
r
_E
of the Earth from the Sun is the sine of
θ
_max
. Here is a table of the angles of maximum elongation, their sines, and the actual orbital radii
r
_P
of Mercury and Venus, in units of the radius
r
_E
of the Earth’s orbit:

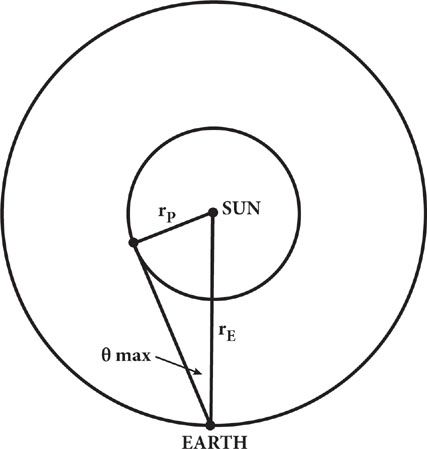
Figure 13. The positions of the Earth and an inner planet (Mercury or Venus) when the planet is at its maximum apparent distance from the Sun.
The circles are the orbits of the Earth and planet.

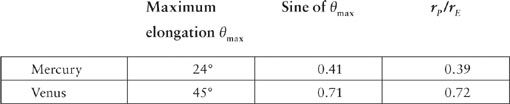
The small discrepancies between the sine of
θ
_max
and the observed ratios
r
_P
/
r
_E
of the orbital radii of the inner planets and the Earth are due to the departure of these orbits from perfect circles with the Sun at the center, and to the fact that the orbits are not in precisely the same plane.

20. Diurnal Parallax

Consider a “new star” or another object that either is at rest with respect to the fixed stars or moves very little relative to the stars in the course of a day. Suppose that it is much closer to Earth than the stars. One can assume that the Earth rotates once a day on its axis from east to west, or that this object and the stars revolve around the Earth once a day from west to east; in either case, because we see the object in different directions at different times of night, its position will seem to shift during every evening
relative to the stars. This is called the “diurnal parallax” of the object. A measurement of the diurnal parallax allows the determination of the distance of the object, or if it is found that the diurnal parallax is too small to be measured, this gives a lower limit to the distance.

To calculate the amount of this angular shift, consider the object’s apparent position relative to the stars seen from a fixed observatory on Earth, when the object just rises above the horizon, and when it is highest in the sky. To facilitate the calculation, we will consider the case that is simplest geometrically: the observatory is on the equator, and the object is in the same plane as the equator. Of course, this does not accurately give the diurnal parallax of the new star observed by Tycho, but it will indicate the order of magnitude of that parallax.

The line to the object from this observatory when the object just rises above the horizon is tangent to the Earth’s surface, so the angle between this line and the line from the observatory to the center of the Earth is a right angle. These two lines, together with the line from the object to the center of the Earth, thus form a right triangle. (See Figure 14.) Angle
θ
(theta) of this triangle at the object has a sine equal to the ratio of the opposite side, the radius
r
_E
of the Earth, to the hypotenuse, the distance
d
of the object from the center of the Earth. As shown in the figure, this angle is also the apparent shift of the position of the object relative to the stars during the time between when it rises above the horizon and when it is highest in the sky. The total shift in its position from when it rises above the horizon to when it sets below the horizon is 2
θ
.

For instance, if we take the object to be at the distance of the Moon, then
d
250,000 miles, while
r
_E
4,000 miles, so sin
θ
4/250, and therefore
θ
0.9°, and the diurnal parallax is 1.8°. From a typical spot on Earth, such as Hven, to an object at a typical location in the sky like the new star of 1572, the diurnal parallax is smaller, but still of the same order of magnitude, in the neighborhood of 1°. This is more than large enough for it to have been detected by a naked-eye astronomer as expert as Tycho Brahe, but Tycho could not detect any diurnal parallax, so he was able to conclude that the new star of 1572 is farther than the Moon. On the other hand, there was no difficulty in measuring the diurnal parallax of the Moon itself, and in this way finding the distance of the Moon from the Earth.