To Explain the World: The Discovery of Modern Science (51 page)

We can solve the equation at the left for
x
:

We then insert this result in the formula for cos
ϕ
, obtaining in this way a relation between
θ
and
ϕ
:

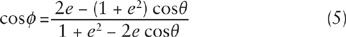
Since both sides of this equation are equal whatever the value of
θ
, the change in the left-hand side must equal the change in the right-hand side when we make any change in
θ
. Suppose we make an infinitesimal change
δθ
(delta theta) in
θ
. To calculate the change in
ϕ
, we make use of a principle in calculus, that when any angle
α
(such as
θ
or
ϕ
) changes by an amount
δα
(delta alpha), the change in cos
α
is –(
δα
/
R
) sin
α
. Also, when any quantity
f
, such as the denominator in Eq. (5), changes by an infinitesimal amount
δf
, the change in 1/
f
is –
δf
/
f
²
. Equating the changes in the two sides of Eq. (5) thus gives

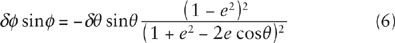
Now we need a formula for the ratio of sin
ϕ
and sin
θ
. For this purpose, note from Figure 15 that the vertical coordinate
y
of a point on the ellipse is given by
y
=
r
₊
sin
θ
and also by
y
=
r
_-
sin
ϕ
, so by eliminating
y
,

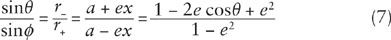
Using this in Eq. (6), we have

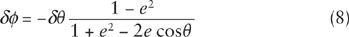
Now, what is the area swept out by the line from the Sun to the planet when the angle
θ
is changed by
δθ
? If we measure angles in degrees, then it is the area of an isosceles triangle with two sides equal to
r
₊
, and the third side equal to the fraction 2
πr
₊
×
δθ
/360° of the circumference 2
πr
₊
of a circle of radius
r
₊
. This area is

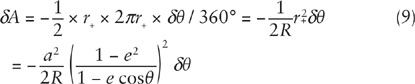
(A minus sign has been inserted here because we want
dA
to be positive when
ϕ
increases; but as we have defined them,
ϕ
increases when
θ
decreases, so
δϕ
is positive when
δθ
is negative.) Thus Eq. (8) may be written

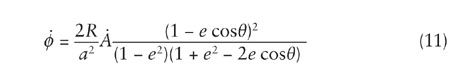
Taking
δA
and
δϕ
to be the area and angle swept out in an infinitesimal time interval
δt
, and dividing Eq. (10) by
δt
, we find a corresponding relation between the rates of sweeping out areas and angles:

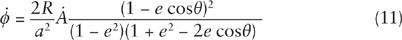
So far, this is all exact. Now let’s consider how this looks when
e
is very small. The numerator of the second fraction in Eq. (11) is (1 –
e
cos
θ
)
²
= 1 – 2
e
cos
θ
+
e
²
cos
²
θ
, so the terms of zeroth and first order in the numerator and denominator of this fraction are the same, the difference between numerator and denominator appearing only in terms proportional to
e
²
. Equation (11) thus immediately yields the desired result, Eq. (1). To be a little more definite, we can keep the terms in Eq. (11) of order
e
²
:

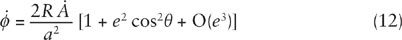
where
O
(
e
³
) denotes terms proportional to
e
³
or higher powers of
e.

22. Focal Length

Consider a vertical glass lens, with a convex curved surface in front and a plane surface in back, like the lens that Galileo and Kepler used as the front end of their telescopes. The curved surfaces that are easiest to grind are segments of spheres, and we will assume that the convex front of the lens is a segment of a sphere of radius
r.
We will also assume throughout that the lens is thin, with a maximum thickness much less than
r.

Suppose that a ray of light traveling in the horizontal direction, parallel to the axis of the lens, strikes the lens at point
P
, and that the line from the center
C
of curvature (behind the lens) to
P
makes an angle
θ
(theta) with the centerline of the lens. The lens will bend the ray of light so that when it emerges from the back of the lens it makes a different angle
ϕ
with the centerline of the lens. The ray will then strike the centerline of the lens at some point
F.
(See Figure 16a.) We are going to calculate the distance
f
of this point from the lens, and show that it is independent of
θ
, so that all horizontal rays of light striking the lens reach the centerline at the same point
F.
Thus we can say that the light striking the lens is focused at point
F
; the distance
f
of this point from the lens is known as the “focal length” of the lens.