To Explain the World: The Discovery of Modern Science (55 page)

This is the same relation between speed and distance fallen
d
=
h
₀
–
h
that holds for a body falling freely, except that
g
has been replaced with
g
/(1 +
ζ
). Aside from this change, the dependence of the velocity of the ball rolling down the inclined plane on the vertical distance traveled is the same as that for a body in free fall. Hence the study of balls rolling down inclined planes could be used to verify that freely falling bodies experience uniform acceleration; but unless the factor 1/(1 +
ζ
) is taken into account, it could not be used to measure the acceleration.

By a complicated argument, Huygens was able to show that the time it takes a pendulum of length
L
to swing through a small angle from one side to the other is

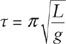
This equals
π
times the time required for a body to fall distance
d
=
L
/2, the result stated by Huygens.

26. Parabolic Trajectories

Suppose a projectile is shot horizontally with speed
v.
Neglecting air resistance, it will continue with this horizontal component of velocity, but it will accelerate downward. Hence after time
t
it will have moved a horizontal distance
x
=
vt
and a downward distance
z
proportional to the square of the time, conventionally written as
z
=
gt
²
/2, with
g
= 32 feet/second per second, a constant measured after Galileo’s death by Huygens. With
t
=
x
/
v
, it follows that

z
=
gx
²
/2
v
²

This equation, giving one coordinate as proportional to the square of the other, defines a parabola.

Note that if the projectile is fired from a gun at height
h
above the ground, then the horizontal distance
x
traveled when the projectile has fallen distance
z
=
h
and reached the ground is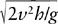
. Even without knowing
v
or
g
, Galileo could have verified that the path of the projectile is a parabola, by measuring the distance traveled
d
for various heights fallen
h
, and checking that
d
is proportional to the square root of
h.
It is not clear whether Galileo ever did this, but there is evidence that in 1608 he did a closely related experiment, mentioned briefly in
Chapter 12
. A ball is allowed to roll down an inclined plane from various initial heights
H
, then rolls along the horizontal tabletop on which the inclined plane sits, and finally shoots off into the air from the table edge. As shown in Technical Note 25, the velocity of the ball at the bottom of the inclined plane is

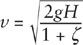
where as usual
g
= 32 feet/second per second, and
ζ
(zeta) is the ratio of rotational to kinetic energy of the ball, a number depending on the distribution of mass within the rolling ball. For a solid ball of uniform density,
ζ
= 2/5. This is also the velocity of the ball when it shoots off horizontally into space from the edge of the tabletop, so the horizontal distance that the ball travels by the time it falls height
h
will be

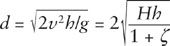
Galileo did not mention the correction for rotational motion represented by
ζ
, but he may have suspected that some such correction could reduce the horizontal distance traveled, because instead of comparing this distance with the value
d
=
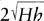expected in the absence of
ζ
, he only checked that for fixed table height
h
, distance
d
was indeed proportional to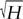
, to an accuracy of a few percent. For one reason or another, Galileo never published the result of this experiment.

For many purposes of astronomy and mathematics, it is convenient to define a parabola as the limiting case of an ellipse, when one focus moves very far from the other. The equation for an ellipse with major axis 2
a
and minor axis 2
b
is given in Technical Note 18 as:

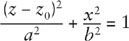
in which for convenience later on we have replaced the coordinates
x
and
y
used in Note 18 with
z
–
z
₀
and
x
, with
z
₀
a constant that can be chosen as we like. The center of this ellipse is at
z
=
z
₀
and
x
= 0. As we saw in Note 18, there is a focus at
z
–
z
₀
= –
ae
,
x
= 0, where
e
is the eccentricity, with
e
²
≡ 1 –
b
²
/
a
²
, and the point of closest approach of the curve to this focus is at
z
–
z
₀
= –
a
and
x
= 0. It will be convenient to give this point of closest approach the coordinates
z
= 0 and
x
= 0 by choosing
z
₀
=
a
and in which case the nearby focus is at
z
=
z
₀
–
ea
= (1 –
e
)
a.
We
want to let
a
and
b
become infinitely large, so that the other focus goes to infinity and the curve has no maximum
x
coordinate, but we want to keep the distance (1 –
e
)
a
of closest approach to the nearer focus finite, so we set

1 −
e
=
ℓ
/
a

with
ℓ
held fixed as
a
goes to infinity. Since
e
approaches unity in this limit, the semiminor axis
b
is given by

b
²
=
a
²
(1 −
e
²
) =
a
²
(1 −
e
)(1 +
e
) → 2
a
²
(1 −
e
) = 2
ℓa

Using
z
₀
=
a
and this formula for
b
²
, the equation for the ellipse becomes