To Explain the World: The Discovery of Modern Science (56 page)

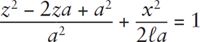
The term
a
²
/
a
²
on the left cancels the 1 on the right. Multiplying the remaining equation with
a
then gives

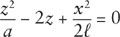
For
a
much larger than
x
,
y
, or
ℓ
, the first term may be dropped, so this equation becomes

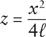
This is the same as the equation we derived for the motion of a projectile fired horizontally, provided we take

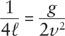
so the focus
F
of the parabola is at distance
ℓ
=
v
²
/2
g
below the initial position of the projectile. (See Figure 19.)

Parabolas can, like ellipses, be regarded as conic sections, but for parabolas the plane intersecting the cone is parallel to the cone’s surface. Taking the equation of a cone centered on the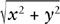
=
α
(
z
+
z
₀
), and the equation of a plane parallel to the cone as simply
y
=
α
(
z
–
z
₀
), with
z
₀
arbitrary, the intersection of the cone and the plane satisfies

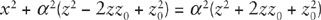
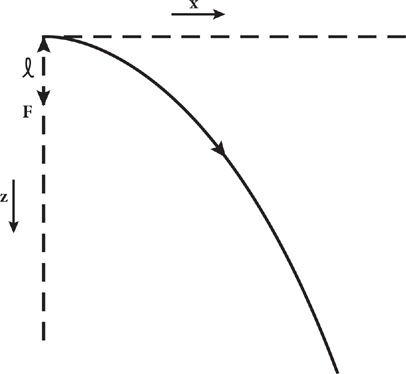
Figure 19. The parabolic path of a projectile that is fired from a hill in a horizontal direction.
Point
F
is the focus of this parabola.

After canceling the terms
α
²
z
²
and
α
²
z
²
₀
, this reads

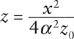
which is the same as our previous result, provided we take
z
₀
=
ℓ
/
α
²
. Note that a parabola of a given shape can be obtained from any cone, with any value of the angular parameter
α
(alpha), because the shape of any parabola (as opposed to its location and orientation) is entirely determined by a parameter
ℓ
with the units of
length; we do not need to know separately any unit-free parameter like
α
or the eccentricity of an ellipse.

27. Tennis Ball Derivation of the Law of Refraction

Descartes attempted a derivation of the law of refraction, based on the assumption that a ray of light is bent in passing from one medium to another in the same way that the trajectory of a tennis ball is bent in penetrating a thin fabric. Suppose a tennis ball with speed
v
_A
strikes a thin fabric screen obliquely. It will lose some speed, so that after penetrating the screen its speed will be
v
_B
<
v
_A
, but we would not expect the ball’s passage through the screen to make any change in the component of the ball’s velocity
along
the screen. We can draw a right triangle whose sides are the components of the ball’s initial velocity perpendicular to the screen and parallel to the screen, and whose hypotenuse is
v
_A
. If the ball’s original trajectory makes an angle
i
to the perpendicular to the screen, then the component of its velocity along the direction parallel to the screen is
v
_A
sin
i.
(See Figure 20.) Likewise, if after penetrating the screen the ball’s trajectory makes an angle
r
with the perpendicular to the screen, then the component of its velocity along the direction parallel to the screen is
v
_B
sin
r.
Using Descartes’ assumption that the passage of the ball through the screen could change only the component of velocity perpendicular to the interface, not the parallel component, we have

v
_A
sin
i
=
v
_B
sin
r

and therefore

where
n
is the quantity: