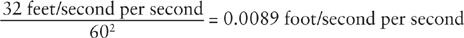To Explain the World: The Discovery of Modern Science (60 page)

Suppose that the distances between us and the planet at two successive times when the moon is at the same stage in its orbit are
d
₁
and
d
₂
. We then observe these stages in the orbit at times

t
ʹ
₁
=
t
₁
+
d
₁
/
c
     
t
ʹ
₂
=
t
₂
+
d
₂
/
c

where
c
is the speed of light. (We are assuming here that the distance between the planet and its moon may be neglected.) If the distance between us and this planet is changing at rate
v
, either
because it is moving or because we are or both, then
d
₂
–
d
₁
=
vT
, and so the observed period is

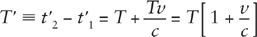
(This derivation depends on the assumption that
v
should change very little in a time
T
, which is typically true in the solar system, but
v
may be changing appreciably over longer time scales.) When the distant planet is moving toward or away from us, in which case
v
is respectively negative or positive, its moon’s apparent period will be decreased or increased, respectively. We can measure
T
by observing the planet at a time when
v
= 0, and then measure the speed of light by observing the period again at a time when
v
has some known nonzero value.

This is the basis of the determination of the speed of light by Huygens, based on Rømer’s observation of the changing apparent orbital period of Jupiter’s moon Io. But with the speed of light known, the same calculation can tell us the relative velocity
v
of a distant object. In particular, the light waves from a specific line in the spectrum of a distant galaxy will oscillate with some characteristic period
T
, related to its frequency
ν
(nu) and wavelength
λ
(lambda) by
T
= 1/
ν
=
λ
/
c.
This intrinsic period is known from observations of spectra in laboratories on Earth. Since the early twentieth century the spectral lines observed in very distant galaxies have been found to have longer wavelengths, and hence longer periods, from which we can infer that these galaxies are moving away from us.

32. Centripetal Acceleration

Acceleration is the rate of change of velocity, but the velocity of any body has both a magnitude, known as the speed, and a direction. The velocity of a body moving on a circle is continually changing its direction, turning toward the circle’s center, so even
at constant speed it undergoes a continual acceleration toward the center, known as its centripetal acceleration.

Let us calculate the centripetal acceleration of a body traveling on a circle of radius
r
, with constant speed
v.
During a short time interval from
t
₁
to
t
₂
, the body will move along the circle by a small distance
vΔt
, where
Δt
(delta
t
) =
t
₂
–
t
₁
, and the radial vector (the arrow from the center of the circle to the body) will swivel around by a small angle
Δθ
(delta theta). The velocity vector (an arrow with magnitude
v
in the direction of the body’s motion) is always tangent to the circle, and hence at right angles to the radial vector, so while the radial vector’s direction changes by an angle
Δθ
, the velocity vector’s direction will change by the same small angle. So we have two triangles: one whose sides are the radial vectors at times
t
₁
and
t
₂
and the chord connecting the positions of the body at these two times; and the other whose sides are the velocity vectors at times
t
₁
and
t
₂
, and the change
Δv
in the velocity between these two times. (See Figure 24.) For small angles
Δθ
, the difference in length between the chord and the arc connecting the positions of the bodies at times
t
₁
and
t
₂
, is negligible, so we can take the length of the chord as
vΔt.

Now, these triangles are similar (that is, they differ in size but not in shape) because they are both isosceles triangles (each has two equal sides) with the same small angle
Δθ
between the two equal sides. So the ratios of the short and long sides of each triangle should be the same. That is

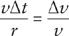
and therefore

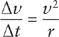
This is Huygens’ formula for the centripetal acceleration.

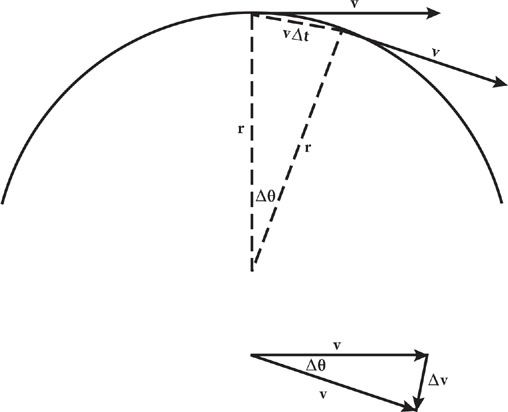
Figure 24. Calculation of centripetal acceleration.
Top: Velocities of a particle moving on a circle at two times, separated by a short time interval Δ
t.
Bottom: These two velocities, brought together into a triangle whose short side is the change of velocity in this time interval.

33. Comparing the Moon with a Falling Body

The ancient supposed distinction between phenomena in the heavens and on Earth was decisively challenged by Newton’s comparison of the centripetal acceleration of the Moon in its orbit with the downward acceleration of a falling body near the surface of the Earth.

From measurements of the Moon’s diurnal parallax, its average distance from the Earth was accurately known in Newton’s time to be 60 times the radius of the Earth. (The actual ratio is
60.27.) To calculate the Earth’s radius Newton took 1' (minute of arc) at the equator to be a mile of 5,000 feet, so with 360° for a circle and 60’ to 1°, the earth’s radius was

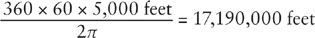
(The mean radius is actually 20,926,300 feet. This was the greatest source of error in Newton’s calculation.) The orbital period of the Moon (the sidereal month) was accurately known to be 27.3 days, or 2,360,000 seconds. The velocity of the Moon in its orbit was then

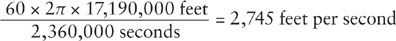
This gives a centripetal acceleration of

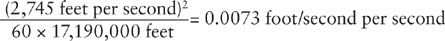
According to the inverse square law, this should have equaled the acceleration of falling bodies on the surface of the Earth, 32 feet/second per second, divided by the square of the ratio of the radius of the Moon’s orbit to the radius of the earth: