To Explain the World: The Discovery of Modern Science (58 page)

The condition that
δL
= 0 tells us that

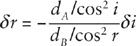
so that

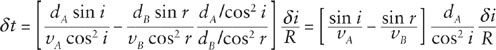
For this to vanish, we must have

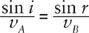
or in other words

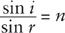
with the index of refraction
n
given by the angle-independent ratio of velocities:

n
=
v
_A
/
v
_B

This is the correct law of refraction, with the correct formula for
n.

29. The Theory of the Rainbow

Suppose that a ray of light arrives at a spherical raindrop at a point
P
, where it makes an angle
i
to the normal to the drop’s surface. If there were no refraction, the light ray would continue straight through the drop. In this case, the line from the center
C
of the drop to the point
Q
of closest approach of the ray to the center would make a right angle with the light ray, so triangle
PCQ
would be a right triangle with hypotenuse equal to the radius
R
of the circle, and the angle at
P
equal to
i.
(See Figure 22a.) The impact parameter
b
is defined as the distance of closest approach of the unrefracted ray to the center, so it is the length of side
CQ
of the triangle, given by elementary trigonometry as

b
=
R
sin
i

We can equally well characterize individual light rays by their value of
b
/
R
, as was done by Descartes, or by the value of the angle of incidence
i.

Because of refraction, the ray will actually enter the drop at angle
r
to the normal, given by the law of refraction:

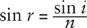
where
n
4/3 is the ratio of the speed of light in air to its speed in water. The ray will cross the drop, and strike its back side at point
p'
. Since the distances from the center
C
of the drop to
P
and to
P'
are both equal to the radius
R
of the drop, the triangle with vertices
C
,
P
, and
P'
is isosceles, so the angles between the light ray and the normals to the surface at
P
and at
P'
must be equal, and hence both equal to
r.
Some of the light will be reflected from the back surface, and by the law of reflection the angle between the reflected ray and the normal to the surface at
P'
will again be
r.
The reflected ray will cross the drop and strike its front surface at a point
P"
, again making an angle
r
with the normal to the surface at
P"
. Some of the light will then emerge from the drop, and
by the law of refraction the angle between the emergent ray and the normal to the surface at
P"
will equal the original incident angle
i.
(See Figure 22b. This figure shows the path of the light ray through a plane parallel to the ray’s original direction that contains the center of the raindrop and the observer. Only rays that impinge on the drop’s surface where it intersects this plane have a chance of reaching the observer.)

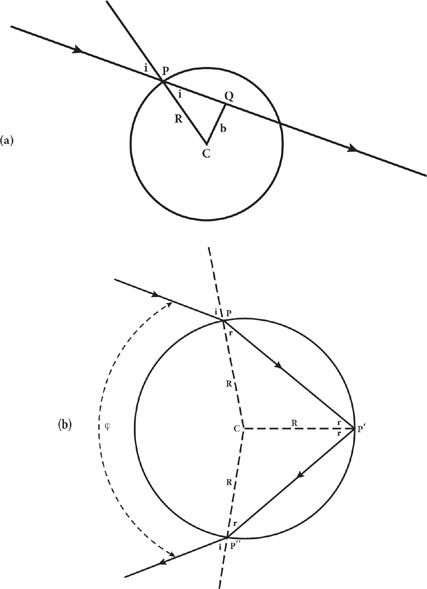
Figure 22. The path of a ray of sunlight in a spherical drop of water.
The ray is indicated by solid lines marked with arrows, and enters the drop at point
P
, where it makes an angle
i
with the normal to the surface. (a) Path of the ray if there were no refraction, with
Q
the point of the ray’s closest approach to the center
C
of the drop in this case. (b) The ray refracted on entering the drop at
P
, reflected from the back surface of the drop at
P
", and then refracted again on leaving the drop at
P
". Dashed lines run from the center
C
of the drop to points where the ray meets the surface of the drop.

In the course of all this bouncing around, the light ray will have been bent toward the center of the drop by an angle
i
–
r
twice on entering and leaving the drop, and by an angle 180° – 2
r
when reflected by the back surface of the drop, and hence by a total angle

2(
i
−
r
) + 180° − 2
r
= 180° − 4
r
+ 2
i

If the light ray bounced straight back from the drop (as is the case for
i
=
r
= 0) this angle would be 180°, and the initial and final light rays would be along the same line, so the actual angle
φ
(phi) between the initial and final light rays is

φ
= 4
r
− 2i

We can express
r
in terms of
i
, as

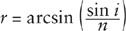
where for any quantity
x
, the quantity arcsin
x
is the angle (usually taken between –90° and +90°) whose sine is
x.
The numerical calculation for
n
= 4/3 reported in
Chapter 13
shows that
φ
rises from zero at
i
= 0 to a maximum value of about 42° and then drops to about 14° at
i
= 90°. The graph of
j
versus
i
is flat at its maximum, so light tends to emerge from the drop at a deflection angle
φ
close to 42°.

If we look up at a misty sky with the sun behind us, we see light reflected back primarily from directions in the sky where the angle between our line of sight and the sun’s rays is near 42°.
These directions form a bow, usually running from the Earth’s surface up into the sky and then down again to the surface. Because
n
depends slightly on the color of light, so does the maximum value of the deflection angle
φ
, so this bow is spread out into different colors. This is the rainbow.

It is not difficult to derive an analytic formula that gives the maximum value of
φ
for any value of the index of refraction
n.
To find the maximum of
φ
, we use the fact that the maximum occurs at an incident angle
i
where the graph of
φ
versus
i
is flat, so that the variation
δφ
(delta phi) in
φ
produced by a small variation
δi
in
i
vanishes to first order in
δi.
To use this condition, we use a standard formula of calculus, which tells us that when we make a change
δx
in
x
, the change in arcsin
x
is