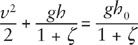To Explain the World: The Discovery of Modern Science (54 page)

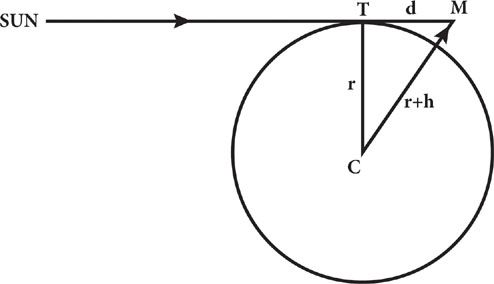
Figure 18. Galileo’s measurement of the height of mountains on the Moon.
The horizontal line marked with an arrow indicates a ray of light that grazes the Moon at the terminator
T
marking the boundary between the Moon’s bright and dark sides, and then strikes the top
M
of a mountain of height
h
at a distance
d
from the terminator.

Galileo in
Siderius Nuncius
reported that he sometimes saw bright spots on the dark side of the Moon at an apparent distance from the terminator greater than 1/20 the apparent diameter of the Moon, so for these mountains
d
/
r
> 1/10, and therefore according to the above formula
h
/
r
> (1/10)
²
/2 = 1/200. Galileo estimated the radius of the Moon to be 1,000 miles,
*
so these mountains would be at least 5 miles high. (For reasons that are not clear, Galileo gave a figure of 4 miles, but since he was trying only to set a lower bound on the mountain height, perhaps he
was just being conservative.) Galileo thought that this was higher than any mountain on the Earth, but now we know that there are mountains on Earth that are almost 6 miles high, so Galileo’s observations indicated that the heights of mountains on the Moon are not very different from the heights of terrestrial mountains.

25. Gravitational Acceleration

Galileo showed that a falling body undergoes uniform acceleration—that is, its speed increases by the same amount in each equal interval of time. In modern terms, a body that falls from rest will after time
t
have a velocity
v
given by a quantity proportional to
t
:

v
=
gt

where
g
is a constant characterizing the gravitational field at the surface of the Earth. Although
g
varies somewhat from place to place on the Earth’s surface, it is never very different from 32 feet/second per second, or 9.8 meters/second per second.

According to the mean speed theorem, the distance that such a body will fall from rest in time
t
is
v
_mean
t
, where
v
_mean
is the average of
gt
and zero; in other words,
v
_mean
=
gt
/2. Hence the distance fallen is

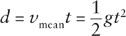
In particular, in the first second the body falls a distance
g
(1 second)
²
/2 = 16 feet. The time required to fall distance
d
is in general

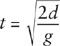
There is another, more modern way of looking at this result. The falling body has an energy equal to the sum of a
kinetic energy
term and a
potential energy
term. The kinetic energy is

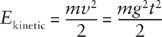
where
m
is the body’s mass. The potential energy is
mg
times the height (measured from any arbitrary altitude), so if the body is dropped from rest at an initial height
h
₀
and falls distance
d
, then

E
_potential
= mgh = mg(h
₀
− d)

Hence with
d
=
gt
2/2, the total energy is a constant:

E = E
_kinetic
+
E
_potential
= mgh
₀

We can turn this around, and derive the relation between velocity and distance fallen by
assuming
the conservation of energy. If we set
E
equal to the value
mgh
₀
that it has at
t
= 0, when
v
= 0 and
h
=
h
₀
, then the conservation of energy gives at all times

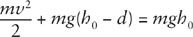
from which it follows that
v
²
/2 =
gd.
Since
v
is the rate of increase of
d
, this is a differential equation that determines the relation between
d
and
t.
Of course, we know the solution of this equation: it is
d
=
gt
²
/2, for which
v
=
gt.
So by using the conservation of energy we can get these results without knowing in advance that the acceleration is uniform.

This is an elementary example of the conservation of energy, which makes the concept of energy useful in a wide variety of contexts. In particular, the conservation of energy shows the relevance of Galileo’s experiments with balls rolling down inclined planes to the problem of free fall, though this is not an argument used by Galileo. For a ball of mass
m
rolling down a plane, the kinetic energy is
mv
²
/2, where
v
is now the velocity
along
the plane, and the potential energy is
mgh
, where
h
is again the height. In addition there is an energy of rotation of the ball, which takes the form

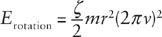
where
r
is the radius of the ball,
ν
(nu) is the number of complete turns of the ball per second, and
ζ
(zeta) is a number that depends on the shape and mass-distribution of the ball. In the case that is probably relevant to Galileo’s experiments, that of a solid uniform ball,
ζ
has the value
ζ
= 2/5. (If the ball were hollow, we would have
ζ
= 2/3.) Now, when the ball makes one complete turn it travels a distance equal to its circumference 2
πr
, so in time
t
when it makes
νt
turns it travels distance
d
= 2
πrνt
, and therefore its velocity is
d
/
t
= 2
πνr.
Using this in the formula for the energy of rotation, we see that

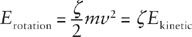
Dividing by
m
and 1 +
ζ
, the conservation of energy therefore requires that