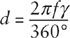To Explain the World: The Discovery of Modern Science (52 page)

First, note that the arc on the front of the lens from the centerline to
P
is a fraction
θ
/360° of the whole circumference 2
πr
of a circle of radius
r.
On the other hand, the same arc is a fraction
ϕ
/360° of the whole circumference 2
πf
of a circle of radius
f.
Since these arcs are the same, we have

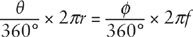
and therefore, canceling factors of 360° and 2
π
,

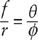
So to calculate the focal length, we need to calculate the ratio of
ϕ
to
θ.

For this purpose, we need to look more closely at what happens to the light ray inside the lens. (See Figure 16b.) The line from the center of curvature
C
to the point
P
where a horizontal light ray strikes the lens is perpendicular to the convex spherical surface of the lens at
P
, so the angle between this perpendicular and the light ray (that is, the angle of incidence) is just
θ
. As was known to Claudius Ptolemy, if
θ
is small (as it will be for a thin
lens), then the angle
α
(alpha) between the ray of light inside the glass and the perpendicular (that is, the angle of refraction) will be proportional to the angle of incidence, so that

α
=
θ
/
n

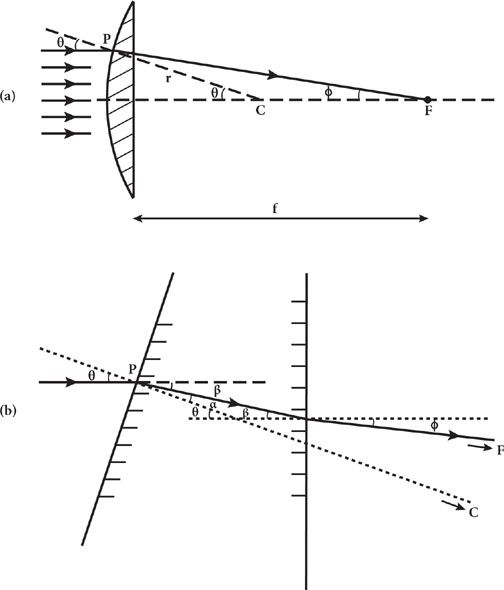
Figure 16. Focal length. (a) Definition of focal length.
The horizontal dashed line is the axis of the lens. Horizontal lines marked with arrows indicate rays of light that enter the lens parallel to this axis. One ray is shown entering the lens at point
P
, where the ray makes a small angle
θ
to a line from the center of curvature
C
that is perpendicular to the convex spherical surface at
P
; this ray is bent by the lens to make an angle
ϕ
to the lens axis and strikes this axis at focal point
F
, at a distance
f
from the lens. This is the focal length. With
ϕ
proportional to
θ
, all horizontal rays are focused to this point. (b) Calculation of focal length. Shown here is a small part of the lens, with the slanted hatched solid line on the left indicating a short segment of the convex surface of the lens. The solid line marked with an arrow shows the path of a ray of light that enters the lens at
P
, where it makes a small angle
θ
to the normal to the convex surface. This normal is shown as a slanted dotted line, a segment of the line from
P
to the center of curvature of the lens, which is beyond the borders of this figure. Inside the lens this ray is refracted so that it makes an angle
α
with this normal, and then is refracted again when it leaves the lens so that it makes an angle
ϕ
with the normal to the planar back surface of the lens. This normal is shown as a dotted line parallel to the axis of the lens.

where
n
> 1 is a constant, known as the “index of refraction,” that depends on the properties of glass and the surrounding medium, typically air. (It was shown by Fermat that
n
is the speed of light in air divided by the speed of light in glass, but this information is not needed here.) The angle
β
(beta) between the light ray inside the glass and the centerline of the lens is then

β
=
θ
−
a
= (1 − 1/
n
)
θ

This is the angle between the light ray and the normal to the flat back surface of the lens when the light ray reaches this surface. On the other hand, when the light ray emerges from the back of the lens it makes a different angle
ϕ
(phi) to the normal to the surface. The relation between
ϕ
and
β
is the same as if the light were going in the opposite direction, in which case
ϕ
would be the angle of incidence and
β
the angle of refraction, so that
β
=
ϕ
/
n
, and therefore

ϕ
=
nβ
= (
n
− 1)
θ

So we see that
ϕ
is simply proportional to
θ
, and therefore, using our previous formula for
f
/
r
, we have

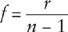
This is independent of
θ
, so as promised all horizontal light rays entering the lens are focused to the same point on the centerline of the lens.

If the radius of curvature
r
is very large, then the curvature of the front surface of the lens is very small, so that the lens is nearly the same as a flat plate of glass, with the bending of light on entering the lens being nearly canceled by its bending on leaving the lens. Similarly, whatever the shape of the lens, if the index of refraction
n
is close to 1, then the lens bends the light ray very little. In either case the focal length is very large, and we say that the lens is
weak.
A
strong
lens is one that has a moderate radius of curvature and an index of refraction appreciably different from 1, as for instance a lens made of glass, for which
n
1.5.

A similar result holds if the back surface of the lens is not plane, but a segment of a sphere of radius
r’
. In this case the focal length is

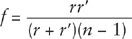
This gives the same result as before if
r’
is much larger than
r
, in which case the back surface is nearly flat.

The concept of focal length can also be extended to concave lenses, like the lens that Galileo used as the eyepiece of his telescope. A concave lens can take rays of light that are converging and spread them out so that they are parallel, or even diverge. We can define the focal length of such a lens by considering converging rays of light that are made parallel by the lens; the focal length is the distance behind the lens of the point to which such rays
would
converge if not made parallel by the lens. Though its meaning is different, the focal length of a concave lens is given by a formula like the one we have derived for a convex lens.

23. Telescopes

As we saw in Technical Note 22, a thin convex lens will focus rays of light that strike it parallel to its central axis to a point
F
on this axis, at a distance behind the lens known as the focal length
f
of the lens. Parallel rays of light that strike the lens at a small angle
γ
(gamma) to the central axis will also be focused by the lens, but to a point that is a little off the central axis. To see how far off, we can imagine rotating the drawing of the ray path in Figure 16a around the lens by angle
γ
. The distance
d
of the focal point from the central axis of the lens will then be the same fraction of the circumference of a circle of radius
f
that
γ
is of 360°:

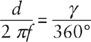
and therefore