To Explain the World: The Discovery of Modern Science (61 page)
Read To Explain the World: The Discovery of Modern Science Online
Authors: Steven Weinberg

It is this comparison, of an “observed” lunar centripetal acceleration of 0.0073 foot/second per second with the value expected from the inverse square law, 0.0089 foot/second per second, to which Newton was referring when he said that they “answer pretty nearly.” He did better later.
34. Conservation of Momentum
Suppose two moving objects with masses
m
1
and
m
2
collide head-on. If in a short time interval
δt
(delta
t
) object 1 exerts
force
F
on object 2, then in this time interval object 2 will experience an acceleration
a
2
that according to Newton’s second law obeys the relation
m
2
a
2
=
F.
Its velocity
v
2
will then change by an amount
δv
2
=
a
2
δt
=
F δt
/
m
2
According to Newton’s third law, particle 2 will exert on particle 1 a force –
F
that is equal in magnitude but (as indicated by the minus sign) opposite in direction, so in the same time interval the velocity
v
1
of object 1 will undergo a change in the opposite direction to
δv
2
, given by
δv
1
=
a
1
δt
= −
F δt
/
m
1
The net change in the total momentum
m
1
v
1
+
m
2
v
2
is then
m
1
δv
1
+
m
2
δv
2
= 0
Of course, the two objects may be in contact for an extended period, during which the force may not be constant, but since the momentum is conserved in every short interval of time, it is conserved during the whole period.
35. Planetary Masses
In Newton’s time four bodies in the solar system were known to have satellites: Jupiter and Saturn as well as the Earth were known to have moons, and all the planets are satellites of the Sun. According to Newton’s law of gravitation, a body of mass
M
exerts a force
F
=
GMm
/
r
2
on a satellite of mass
m
at distance
r
(where
G
is a constant of nature), so according to Newton’s second law of motion the centripetal acceleration of the satellite will be
a
=
F
/
m
=
GM
/
r
2
. The value of the constant
G
and the overall scale of the solar system were not known in Newton’s
time, but these unknown quantities do not appear in the
ratios
of masses calculated from ratios of distances and ratios of centripetal accelerations. If two satellites of bodies with masses
M
1
and
M
2
are found to be at distances from these bodies with a known ratio
r
1
/
r
2
and to have centripetal accelerations with a known ratio
a
1
/
a
2
, then the ratio of the masses can be found from the formula
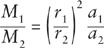
In particular, for a satellite moving at constant speed
v
in a circular orbit of radius
r
the orbital period is
T
= 2
πr
/
v
, so the centripetal acceleration
v
2
/
r
is
a
= 4
π
2
r
/
T
2
, the ratio of accelerations is
a
1
/
a
2
= (
r
1
/
r
2
)/(
T
2
/
T
1
)
2
, and the ratio of masses inferred from orbital periods and ratios of distances is
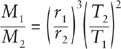
By 1687 all the
ratios
of the distances of the planets from the Sun were well known, and from the observation of the angular separation of Jupiter and Saturn from their moons Callisto and Titan (which Newton called the “Huygenian satellite”) it was also possible to work out the ratio of the distance of Callisto from Jupiter to the distance of Jupiter from the Sun, and the ratio of the distance of Titan from Saturn to the distance of Saturn from the Sun. The distance of the Moon from the Earth was quite well known as a multiple of the size of the Earth, but
not
as a fraction of the distance of the Earth from the Sun, which was then not known. Newton used a crude estimate of the ratio of the distance of the Moon from the Earth and the distance of the Earth from the Sun, which turned out to be badly in error. Aside from this problem, the ratios of velocities and centripetal accelerations could be calculated from the known orbital periods of planets and moons. (Newton actually used the period of Venus rather than of Jupiter or Saturn, but this was just as useful
because the ratios of the distances of Venus, Jupiter, and Saturn from the Sun were all well known.) As reported in
Chapter 14
, Newton’s results for the ratios of the masses of Jupiter and Saturn to the mass of the Sun were reasonably accurate, while his result for the ratio of the mass of the Earth to the mass of the Sun was badly in error.
PART I: GREEK PHYSICS
1. Matter and Poetry
1
. Aristotle,
Metaphysics
, Book I, Chapter 3, 983b 6, 20 (Oxford trans.). Here and below I follow the standard practice of citing passages from Aristotle by referring to their location in I. Bekker’s 1831 Greek edition. By “Oxford trans.,” I mean that the English language version is taken from
The Complete Works of Aristotle—The Revised Oxford Translation
, ed. J. Barnes (Princeton University Press, Princeton, N.J., 1984), which uses this convention in citing passages from Aristotle.
2
. Diogenes Laertius,
Lives of the Eminent Philosophers
, Book I, trans. R. D. Hicks (Loeb Classical Library, Harvard University Press, Cambridge, Mass., 1972), p. 27.
3
. From J. Barnes,
The Presocratic Philosophers
, rev. ed. (Routledge and Kegan Paul, London, 1982), p. 29. The quotations in this work, hereafter cited as
Presocratic Philosophers
, are translations into English of the fragmentary quotations in the standard sourcebook by Hermann Diels and Walter Kranz,
Die Fragmente der Vorsokratiker
(10th ed., Berlin, 1952).
4
.
Presocratic Philosophers
, p. 53.
5
. From J. Barnes,
Early Greek Philosophy
(Penguin, London, 1987), p. 97. Hereafter cited as
Early Greek Philosophy.
As in
Presocratic Philosophers
, these quotations are taken from Diels and Kranz, 10th ed.
6
. From K. Freeman,
The Ancilla to the Pre-Socratic Philosophers
(Harvard University Press, Cambridge, Mass., 1966), p. 26.
Hereafter cited as
Ancilla.
This is a translation into English of the quotations in Diels,
Fragmente der Vorsokratiker
, 5th ed.
7
.
Ancilla
, p. 59.
8
.
Early Greek Philosophy
, p. 166.
9
. Ibid., p. 243.
10
.
Ancilla
, p. 93.
11
. Aristotle,
Physics
, Book VI, Chapter 9, 239b 5 (Oxford trans.).
12
. Plato,
Phaedo
, 97C–98C. Here and below I follow the standard practice of citing passages from Plato’s works by giving page numbers in the 1578 Stephanos Greek edition.
13
. Plato,
Timaeus
, 54 A–B, from Desmond Lee, trans.,
Timaeus and Critias
(Penguin Books, London, 1965).
14
. For instance, in the Oxford translation of Aristotle’s
Physics
, Book IV, Chapter 6, 213b 1–2.
15
.
Ancilla
, p. 24.
16
.
Early Greek Philosophy
, p. 253.
17
. I have written about this point at greater length in the chapter “Beautiful Theories” in
Dreams of a Final Theory
(Pantheon, New York, 1992; reprinted with a new afterword, Vintage, New York, 1994).
2. Music and Mathematics
1
. For the provenance of these stories, see Alberto A. Martínez,
The Cult of Pythagoras—Man and Myth
(University of Pittsburgh Press, Pittsburgh, Pa., 2012).
2
. Aristotle,
Metaphysics
, Book I, Chapter 5, 985b 23–26 (Oxford trans.).
3
. Ibid., 986a 2 (Oxford trans.).
4
. Aristotle,
Prior Analytics
, Book I, Chapter 23, 41a 23–30.
5
. Plato,
Theaetetus
, 147 D–E (Oxford trans.).
6
. Aristotle,
Physics
, 215
p
1–5 (Oxford trans.).
7
. Plato,
The Republic
, 529E, trans. Robin Wakefield (Oxford University Press, Oxford, 1993), p. 261.
8
. E. P. Wigner, “The Unreasonable Effectiveness of Mathematics,”
Communications in Pure and Applied Mathematics
13
(1960): 1–14.
3. Motion and Philosophy
1
. J. Barnes, in
The Complete Works of Aristotle—The Revised Oxford Translation
(Princeton University Press, Princeton, N.J., 1984).
2
. R. J. Hankinson, in
The Cambridge Companion to Aristotle
, ed. J. Barnes (Cambridge University Press, Cambridge, 1995), p. 165.