To Explain the World: The Discovery of Modern Science (46 page)

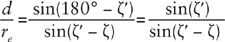
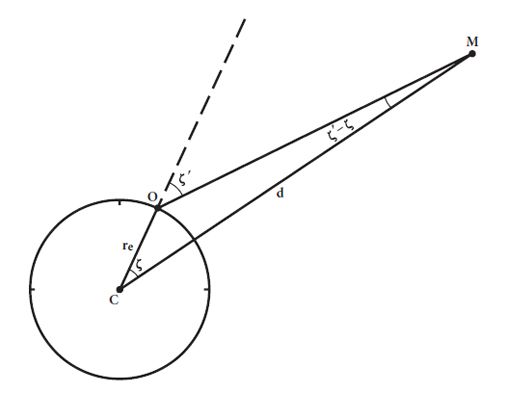
Figure 8. Use of parallax to measure the distance to the Moon.
Here
ζ
’ is the observed angle between the line of sight to the Moon and the vertical direction, and
ζ
is the value this angle would have if the Moon were observed from the center of the Earth.

On October 1, AD 135, Ptolemy observed that the zenith angle of the Moon as seen from Alexandria was
ζʹ
= 50°55’, and his calculations showed that at the same moment the corresponding angle that would be observed from the center of the Earth was
ζ
= 49°48’. The relevant sines are

sinζʹ = 0.776   sin(ζʹ − ζ) = 0.0195

From this Ptolemy could conclude that the distance from the center of the Earth to the Moon in units of the radius of the Earth is

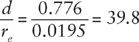
This was considerably less than the actual ratio, which on average is about 60. The trouble was that the difference
ζʹ
–
ζ
was not actually known accurately by Ptolemy, but at least it gave a good idea of the order of magnitude of the distance to the Moon.

Anyway, Ptolemy did better than Aristarchus, from whose values for the ratio of the diameters of the Earth and Moon and of the distance and diameter of the Moon he could have inferred that
d
/
r
_e
is between 215/9 = 23.9 and 57/4 = 14.3. But if Aristarchus had used a correct value of about 1/2° for the angular diameter of the Moon’s disk instead of his value of 2° he would have found
d
/
r
_e
to be four times greater, between 57.2 and 95.6. That range includes the true value.

15. Sines and Chords

The mathematicians and astronomers of antiquity could have made great use of a branch of mathematics known as trigonometry, which is taught today in high schools. Given any angle of a right triangle (other than the right angle itself) trigonometry tells us how to calculate the ratios of the lengths of all the sides. In particular, the side opposite the angle divided by the hypotenuse is a quantity known as the “sine” of that angle, which can be found by looking it up in mathematical tables or typing the angle in a hand calculator and pressing “sin.” (The side of the triangle adjacent to an angle divided by the hypotenuse is the “cosine” of the angle, and the side opposite divided by the side adjacent is the “tangent” of the angle, but it will be enough for us to deal here with sines.) Though no notion of a sine appears anywhere in Hellenistic mathematics, Ptolemy’s
Almagest
makes use of a related quantity, known as the “chord” of an angle.

To define the chord of an angle
θ
(theta), draw a circle of radius 1 (in whatever units of length you find convenient), and draw
two radial lines from the center to the circumference, separated by that angle. The chord of the angle is the length of the straight line, or chord, that connects the points where the two radial lines intersect the circumference. (See Figure 9.) The
Almagest
gives a table of chords
*
in a Babylonian sexigesimal notation, with angles expressed in degrees of arc, running from 1/2° to 180°. For instance, the chord of 45° is given as 45 15 19, or in modern notation

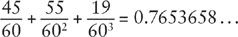
while the true value is 0.7653669. . . .

The chord has a natural application to astronomy. If we imagine the stars as lying on a sphere of radius equal to 1, centered on the center of the Earth, then if the lines of sight to two stars are separated by angle
θ
, the apparent straight-line distance between the stars will be the chord of
θ
.

To see what these chords have to do with trigonometry, return to the figure used to define the chord of angle
θ
, and draw a line (the dashed line in Figure 9) from the center of the circle that just bisects the chord. We then have two right triangles, each with an angle at the center of the circle equal to
θ
/2, and a side opposite this angle whose length is half the chord. The hypotenuse of each of these triangles is the radius of the circle, which we are taking to be 1, so the sine of
θ
/2, in mathematical notation sin(
θ
/2), is half the chord of
θ
, or:

chord of
θ
= 2sin(
θ
/2)

Hence any calculation that can be done with sines can also be done with chords, though in most cases less conveniently.

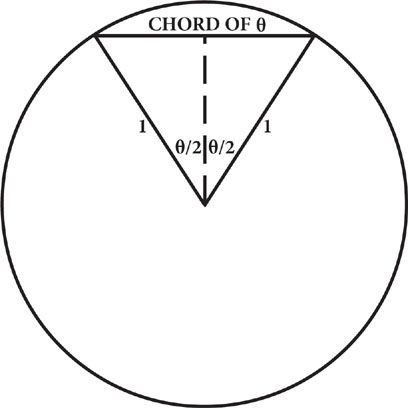
Figure 9. The chord of an angle
θ
.
The circle here has a radius equal to 1. The solid radial lines make an angle
θ
at the center of the circle; the horizontal line runs between the intersections of these lines with the circle; and its length is the chord of this angle.

16. Horizons

Normally our vision outdoors is obstructed by nearby trees or houses or other obstacles. From the top of a hill, on a clear day, we can see much farther, but the range of our vision is still restricted by a horizon, beyond which lines of sight are blocked by the Earth itself. The Arab astronomer al-Biruni described a clever method for using this familiar phenomenon to measure the radius of the Earth, without needing to know any distances other than the height of the mountain.

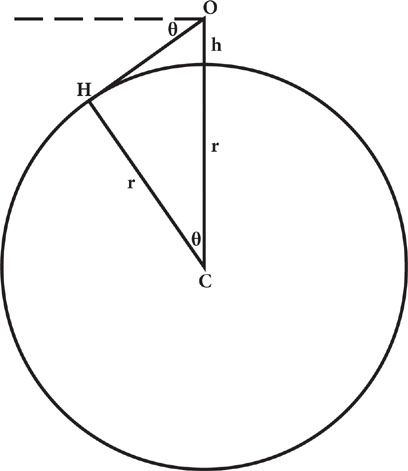
Figure 10. Al-Biruni’s use of horizons to measure the size of the Earth.
O
is an observer on a hill of height
h
;
H
is the horizon as seen by this observer; the line from
H
to
O
is tangent to the Earth’s surface at
H
, and therefore makes a right angle with the line from the center
C
of the Earth to
H.

An observer
O
on top of a hill can see out to a point
H
on the Earth’s surface, where the line of sight is tangent to the surface. (See Figure 10.) This line of sight is at right angles to the line joining
H
to the Earth’s center
C
, so triangle
OCH
is a right triangle. The line of sight is not in the horizontal direction, but below the horizontal direction by some angle
θ
, which is small because the Earth is large and the horizon far away. The angle between the line of sight and the vertical direction at the hill is then 90° –
θ
, so since the sum of the angles of any triangle must be 180°, the acute angle of the triangle at the center of the Earth is 180° – 90° – (90° –
θ
) =
θ
. The side of the triangle adjacent to this angle is the
line from
C
to
H
, whose length is the Earth’s radius
r
, while the hypotenuse of the triangle is the distance from
C
to
O
, which is
r
+
h
, where
h
is the height of the mountain. According to the general definition of the cosine, the cosine of any angle is the ratio of the adjacent side to the hypotenuse, which here gives

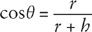
To solve this equation for
r
, note that its reciprocal gives 1 +
h
/
r
= 1/cos
θ
, so by subtracting 1 from this equation and then taking the reciprocal again we have