To Explain the World: The Discovery of Modern Science (42 page)

1, 2, 1/2, 3, 1/3, 2/3, 3/2, 4, 1/4, 3/4, 4/3, . . .

while no such list of all irrational numbers is possible.

6. Terminal Velocity

To understand how observations of falling bodies might have led Aristotle to his ideas about motion, we can make use of a physical principle unknown to Aristotle, Newton’s second law of motion. This principle tells us that the acceleration
a
of a body (the rate at which its speed increases) equals the total force
F
acting on the body divided by the body’s mass
m
:

a
=
F
/
m

There are two main forces that act on a body falling through the air. One is the force of gravity, which is proportional to the body’s mass:

F
_grav
=
mg

Here
g
is a constant independent of the nature of the falling body. It equals the acceleration of a falling body that is subject only to gravity, and has the value 32 feet/second per second on and near the Earth’s surface. The other force is the resistance of the air. This is a quantity
f
(
v
) proportional to the density of the air, which increases with velocity and also depends on the body’s shape and size, but does not depend on its mass:

F
_air
= −
f
(
v
)

A minus sign is put in this formula for the force of air resistance because we are thinking of acceleration in a downward direction, and for a falling body the force of air resistance acts upward, so with this minus sign in the formula,
f
(
v
) is positive. For instance, for a body falling through a sufficiently viscous fluid, the air resistance is proportional to velocity

f
(
v
) =
kv

with
k
a positive constant that depends on the body’s size and shape. For a meteor or a missile entering the thin air of the upper atmosphere, we have instead

f
(
v
) =
Kv
²

with
K
another positive constant.

Using the formulas for these forces in the total force
F
=
F
_grav
+
F
_air
and using the result in Newton’s law, we have

a
=
g
−
f
(
v
)/
m

When a body is first released, its velocity vanishes, so there is no air resistance, and its acceleration downward is just
g.
As time passes its velocity increases, and air resistance begins to reduce its acceleration. Eventually the velocity approaches a value where the term –
f
(
v
)/
m
just cancels the term
g
in the formula for acceleration, and the acceleration becomes negligible. This is the terminal velocity, defined as the solution of the equation:

f
(
v
_terminal
) =
gm

Aristotle never spoke of terminal velocity, but the velocity given by this formula has some of the same properties that he attributed to the velocity of falling bodies. Since
f
(
v
) is an increasing function of
v
, the terminal velocity increases with the mass
m.
In the special case where
f
(
v
) =
kv
, the terminal velocity is simply proportional to the mass and inversely proportional to the air resistance:

v
_terminal
=
gm
/
k

But these are not general properties of the velocity of falling bodies; heavy bodies do not reach terminal velocity until they have fallen for a long time.

7. Falling Drops

Strato observed that falling drops get farther and farther apart as they fall, and concluded from this that these drops accelerate downward. If one drop has fallen farther than another, then it has been falling longer, and if the drops are separating, then the one that is falling longer must also be falling faster, showing that its fall is accelerating. Though Strato did not know it, the
acceleration is constant, and as we shall see, this results in a separation between drops that is proportional to the time elapsed.

As mentioned in Technical Note 6, if air resistance is neglected, then the acceleration downward of any falling body is a constant
g
, which in the neighborhood of the Earth’s surface has the value 32 feet/second per second. If a body falls from rest, then after a time interval
τ
(tau) its velocity downward will be
gτ
. Hence if drops 1 and 2 fall from rest from the same downspout at times
t
₁
and
t
₂
, then at a later time
t
the speed downward of these drops with be
v
₁
=
g
(
t
–
t
₁
) and
v
₂
=
g
(
t
–
t
₂
), respectively. The difference in their speeds will therefore be

v
₁
−
v
₂
=
g
(
t
−
t
₁
) −
g
(
t
−
t
₂
) =
g
(
t
₂
−
t
₁
)

Although both
v
₁
and
v
₂
are increasing with time, their difference is independent of the time
t
, so the separation
s
between the drops simply increases in proportion to the time:

s
= (
v
₁
−
v
₂
)
t
=
gt
(
t
₁
−
t
₂
)

For instance, if the second drop leaves the downspout a tenth of a second after the first drop, then after half a second the drops will be 32 × 1/2 × 1/10 = 1.6 feet apart.

8. Reflection

The derivation of the law of reflection by Hero of Alexandria was one of the earliest examples of the mathematical deduction of a physical principle from a deeper, more general, principle. Suppose an observer at point
A
sees the reflection in a mirror of an object at point
B.
If the observer sees the image of the object at a point
P
on the mirror, the light ray must have traveled from
B
to
P
and then to
A.
(Hero probably would have said that the light traveled from the observer at
A
to the mirror and then to
the object at
B
, as if the eye reached out to touch the object, but this makes no difference in the argument below.) The problem of reflection is: where on the mirror is
P
?

To answer this question, Hero assumed that light always takes the shortest possible path. In the case of reflection, this implies that
P
should be located so that the total length of the path from
B
to
P
and then to
A
is the shortest path that goes from
B
to anywhere on the mirror and then to
A.
From this, he concluded that angle
θ
_i
(theta
_i
) between the mirror and the incident ray (the line from
B
to the mirror) equals angle
θ
_r
between the mirror and the reflected ray (the line from the mirror to
A
).

Here is the proof of the equal-angles rule. Draw a line perpendicular to the mirror from
B
to a point
Bʹ
that is as far behind the mirror as
B
is in front of the mirror. (See Figure 3.) Suppose that this line intersects the mirror at point
C.
Sides
BʹC
and
CP
of right triangle
BʹCP
have the same lengths as sides
BC
and
CP
of right triangle
BCP
, so the hypotenuses
BʹP
and
BP
of these two triangles must also have the same length. The total distance traveled by the light ray from
B
to
P
and then to
A
is therefore the same as the distance that would be traveled by the light ray if it went from
Bʹ
to
P
and then to
A.
The shortest distance between points
Bʹ
and
A
is a straight line, so the path that minimizes the total distance between the object and the observer is the one for which
P
is on the straight line between
Bʹ
and
A.
When two straight lines intersect, the angles on opposite sides of the intersection point are equal, so angle
θ
between line
BʹP
and the mirror equals angle
θ
_r
between the reflected ray and the mirror. But because the two right triangles
BʹCP
and
BCP
have the same sides, angle
θ
must also equal angle
θ
_i
between the incident ray
BP
and the mirror. So, since both
θ
_i
and
θ
_r
are equal to
θ
, they are equal to each other. This is the fundamental equal-angles rule that determines the location
P
on the mirror of the image of the object.

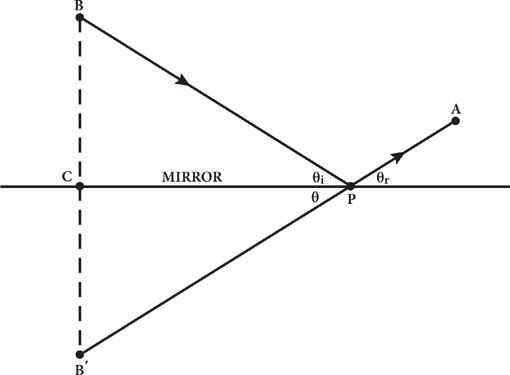
Figure 3. Proof of Hero’s theorem.
This theorem states that the shortest path from an object at
B
to the mirror and then to an eye at
A
is one for which angles
θ
_i
and
θ
_r
are equal. The solid lines marked with arrows represent the path of a light ray; the horizontal line is the mirror; and the dashed line is a line perpendicular to the mirror that runs from
B
to a point
B'
on the other side of the mirror at an equal distance from it.

9. Floating and Submerged Bodies

In his great work
On Floating Bodies
, Archimedes assumed that if bodies are floating or suspended in water in such a way that equal areas at equal depths in the water are pressed down by different weights, then the water and the bodies will move until all equal areas at any given depth are pressed down by the same weight. From this assumption, he derived general consequences about both floating and submerged bodies, some of which were even of practical importance.

First, consider a body like a ship whose weight is less than the weight of an equal volume of water. The body will float on the surface of the water, and displace some quantity of water. If we mark out a horizontal patch in the water at some depth directly below the floating body, with an area equal to the area of the body at its waterline, then the weight pressing down on this surface will be the weight of the floating body plus the weight of the water above that patch, but not including the water displaced by the body, as this water is no longer above the patch. We can compare this with the weight pressing down on an equal area at an equal depth, away from the location of the floating body. This of course does not include the weight of the floating body, but it does include all the water from this patch to the surface, with no water displaced. In order for both patches to be pressed down by the same weight, the weight of the water displaced by the floating body must equal the weight of the floating body. This is why the weight of a ship is referred to as its “displacement.”