Data Mining (49 page)

Nisbet, R., J. Elder, G. Miner,
Handbook of Statistical Analysis and Data Mining Applications
, Elsevier Inc., Amsterdam, 2009.

The book is a comprehensive professional reference book that guides business analysts, scientists, engineers, and researchers (both academic and industrial) through all stages of data analysis, model building, and implementation. The handbook helps one discern technical and business problems, understand the strengths and weaknesses of modern data-mining algorithms, and employ the right statistical methods for practical application. Use this book to address massive and complex data sets with novel statistical approaches and be able to objectively evaluate analyses and solutions. It has clear, intuitive explanations of the principles and tools for solving problems using modern analytic techniques, and discusses their application to real problems, in ways accessible and beneficial to practitioners across industries—from science and engineering, to medicine, academia, and commerce. This handbook brings together, in a single resource, all the information a beginner will need to understand the tools and issues in data mining to build successful data-mining solutions.

Chapter Objectives

• Analyze the characteristics of a logic-based approach to classification problems.
  
• Describe the differences between decision-tree and decision-rule representations in a final classification model.
  
• Explain in-depth the C4.5 algorithm for generating decision trees and decision rules.
  
• Identify the required changes in the C4.5 algorithm when missing values exist in training or testing data set.
  
• Introduce the basic characteristics of Classification and Regression Trees (CART) algorithm and Gini index.
  
• Know when and how to use pruning techniques to reduce the complexity of decision trees and decision rules.
  
• Summarize the limitations of representing a classification model by decision trees and decision rules.
  

Decision trees and decision rules are data-mining methodologies applied in many real-world applications as a powerful solution to classification problems. Therefore, to be begin with, let us briefly summarize the basic principles of classification. In general, classification is a process of learning a function that maps a data item into one of several predefined classes. Every classification based on inductive-learning algorithms is given as an input a set of samples that consist of vectors of attribute values (also called feature vectors) and a corresponding class. The goal of learning is to create a classification model, known as a
classifier
, which will predict, with the values of its available input attributes, the class for some entity (a given sample). In other words, classification is the process of assigning a discrete label value (class) to an unlabeled record, and a classifier is a model (a result of classification) that predicts one attribute—class of a sample—when the other attributes are given. In doing so, samples are divided into predefined groups. For example, a simple classification might group customer billing records into two specific classes: those who pay their bills within 30 days and those who takes longer than 30 days to pay. Different classification methodologies are applied today in almost every discipline where the task of classification, because of the large amount of data, requires automation of the process. Examples of classification methods used as a part of data-mining applications include classifying trends in financial market and identifying objects in large image databases.

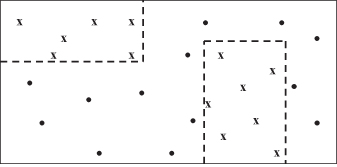
A more formalized approach to classification problems is given through its graphical interpretation. A data set with n features may be thought of as a collection of discrete points (one per example) in an n-dimensional space. A classification rule is a hypercube that contains one or more of these points. When there is more than one cube for a given class, all the cubes are OR-ed to provide a complete classification for the class, such as the example of two-dimensional (2-D) classes in Figure
6.1
. Within a cube the conditions for each part are AND-ed. The size of a cube indicates its generality, that is, the larger the cube is, the more vertices it contains and potentially covers more sample points.

Figure 6.1.
Classification of samples in a 2-D space.

In a classification model, the connection between classes and other properties of the samples can be defined by something as simple as a flowchart or as complex and unstructured as a procedure manual. Data-mining methodologies restrict discussion to formalized, “executable” models of classification, and there are two very different ways in which they can be constructed. On the one hand, the model might be obtained by interviewing the relevant expert or experts, and most knowledge-based systems have been built this way despite the well-known difficulties in taking this approach. Alternatively, numerous recorded classifications might be examined and a model constructed inductively by generalizing from specific examples that are of primary interest for data-mining applications.

The statistical approach to classification explained in Chapter 5 gives one type of model for classification problems: summarizing the statistical characteristics of the set of samples. The other approach is based on logic. Instead of using math operations like addition and multiplication, the logical model is based on expressions that are evaluated as true or false by applying Boolean and comparative operators to the feature values. These methods of modeling give accurate classification results compared with other nonlogical methods, and they have superior explanatory characteristics. Decision trees and decision rules are typical data-mining techniques that belong to a class of methodologies that give the output in the form of logical models.

6.1 DECISION TREES

A particularly efficient method of producing classifiers from data is to generate a decision tree. The decision-tree representation is the most widely used logic method. There is a large number of decision-tree induction algorithms described primarily in the machine-learning and applied-statistics literature. They are supervised learning methods that construct decision trees from a set of input–output samples. It is an efficient nonparametric method for classification and regression. A decision tree is a hierarchical model for supervised learning where the
local region
is identified in a sequence of recursive
splits
through decision nodes with test function. A decision tree is also a nonparametric model in the sense that we
do not assume any parametric form
for the class density.

A typical decision-tree learning system adopts a top-down strategy that searches for a solution in a part of the search space. It guarantees that a simple, but not necessarily the simplest, tree will be found. A decision tree consists of
nodes
where attributes are tested. In a univariate tree, for each internal node, the test uses only one of the attributes for testing. The outgoing
branches
of a node correspond to all the possible outcomes of the test at the node. A simple decision tree for classification of samples with two input attributes X and Y is given in Figure
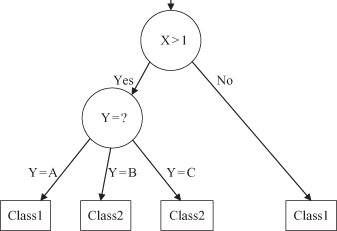
6.2
. All samples with feature values X > 1 and Y = B belong to Class2, while the samples with values X < 1 belong to Class1, whatever the value for feature Y is. The samples, at a non-leaf node in the tree structure, are thus partitioned along the branches and each child node gets its corresponding subset of samples. Decision trees that use univariate splits have a simple representational form, making it relatively easy for the user to understand the inferred model; at the same time, they represent a restriction on the expressiveness of the model. In general, any restriction on a particular tree representation can significantly restrict the functional form and thus the approximation power of the model. A well-known tree-growing algorithm for generating decision trees based on univariate splits is Quinlan’s
ID3
with an extended version called
C4.5
. Greedy search methods, which involve growing and pruning decision-tree structures, are typically employed in these algorithms to explore the exponential space of possible models.

Figure 6.2.
A simple decision tree with the tests on attributes X and Y.

The ID3 algorithm starts with all the training samples at the root node of the tree. An attribute is selected to partition these samples. For each value of the attribute a branch is created, and the corresponding subset of samples that have the attribute value specified by the branch is moved to the newly created child node. The algorithm is applied recursively to each child node until all samples at a node are of one class. Every path to the leaf in the decision tree represents a classification rule. Note that the critical decision in such a top-down decision tree-generation algorithm is the choice of an attribute at a node. Attribute selection in ID3 and C4.5 algorithms are based on minimizing an information entropy measure applied to the examples at a node. The approach based on information entropy insists on minimizing the number of tests that will allow a sample to classify in a database. The attribute-selection part of ID3 is based on the assumption that the complexity of the decision tree is strongly related to the amount of information conveyed by the value of the given attribute. An information-based heuristic selects the attribute providing the highest information gain, that is, the attribute that minimizes the information needed in the resulting subtree to classify the sample. An extension of ID3 is the C4.5 algorithm, which extends the domain of classification from categorical attributes to numeric ones. The measure favors attributes that result in partitioning the data into subsets that have a low-class entropy, that is, when the majority of examples in it belong to a single class. The algorithm basically chooses the attribute that provides the maximum degree of discrimination between classes locally. More details about the basic principles and implementation of these algorithms will be given in the following sections.

To apply some of the methods, which are based on the inductive-learning approach, several key requirements have to be satisfied:

6.2 C4.5 ALGORITHM: GENERATING A DECISION TREE

The most important part of the C4.5 algorithm is the process of generating an initial decision tree from the set of training samples. As a result, the algorithm generates a classifier in the form of a decision tree: a structure with two types of nodes—
a leaf
indicating a class, or
a decision node
specifying some tests to be carried out on a single-attribute value, with one branch and a subtree for each possible outcome of the test.

A decision tree can be used to classify a new sample by starting at the root of the tree and moving through it until a leaf is encountered. At each non-leaf decision node, the features’ outcome for the test at the node is determined and attention shifts to the root of the selected subtree. For example, if the classification model of the problem is given with the decision tree in Figure
6.3
a, and the sample for classification in Figure
6.3
b, then the algorithm will create the path through the nodes
A
,
C
, and
F
(leaf node) until it makes the final classification decision:
CLASS2
.